
【题目】如图,已知点C在⊙O上,AC=![]() AB,动点P与点C位于直径AB的异侧,点P在半圆弧AB上运动(不与A.B两点重合),连结BP,过点C作直线PB的垂线CD交直线PB于D点,连结CP.
AB,动点P与点C位于直径AB的异侧,点P在半圆弧AB上运动(不与A.B两点重合),连结BP,过点C作直线PB的垂线CD交直线PB于D点,连结CP.
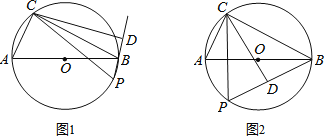
(1)如图1,在点P运动过程中,求∠CPD的度数;
(2)如图2,在点P运动过程中,当CP⊥AB时,AC=2时,求△BPC的周长
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某县有A、B两个大型蔬菜基地,共有蔬菜700吨.若将A基地的蔬菜全部运往甲市所需费用与B基地的蔬菜全部运往甲市所需费用相同.从A、B两基地运往甲、乙两市的运费单价如下表:
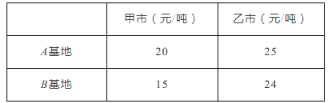
(1)求A、B两个蔬菜基地各有蔬菜多少吨?
(2)现甲市需要蔬菜260吨,乙市需要蔬菜440吨.设从A基地运送![]() 吨蔬菜到甲市,请问怎样调运可使总运费最少?
吨蔬菜到甲市,请问怎样调运可使总运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把线段BD 绕着点D逆时针旋转α(0<α<180)度后,如果点B恰好落在Rt△ABC的边上,那么α=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
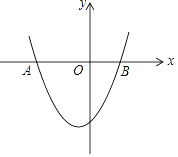
【题目】如图,已知抛物线y=x2+x﹣6与x轴两个交点分别是A、B(点A在点B的左侧).
(1)求A、B的坐标;
(2)利用函数图象,写出y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小英同时掷甲、乙两个质地均匀的骰子(6个面上分别标有1,2,3,4,5,6这6个数字).记甲朝上的一面数字为x,乙朝上的一面数字为y,这样确定点P的一个坐标(x,y),那么点P落在y=![]() 上的概率是_____.
上的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
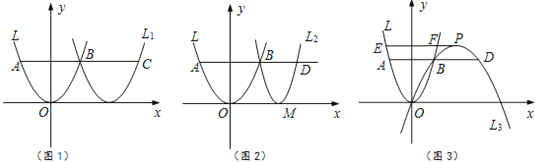
【题目】在平面直角坐标系中,点O为原点,平行于x轴的直线与抛物线L:y=ax2相交于A,B两点(点B在第一象限),点D在AB的延长线上.
(1)已知a=1,点B的纵坐标为2.
①如图1,向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,求AC的长.
②如图2,若BD=![]() AB,过点B,D的抛物线L2,其顶点M在x轴上,求该抛物线的函数表达式.
AB,过点B,D的抛物线L2,其顶点M在x轴上,求该抛物线的函数表达式.
(2)如图3,若BD=AB,过O,B,D三点的抛物线L3,顶点为P,对应函数的二次项系数为a3,过点P作PE∥x轴,交抛物线L于E,F两点,求![]() 的值,并直接写出
的值,并直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD 中,AB=4,AD=a,点P在AD上,且AP=2,点E是边AB上的动点,以PE为边作直角∠EPF,射线PF交BC于点F,连接EF,给出下列结论:①tan∠PFE=![]() ;②a的最小值为10.则下列说法正确的是( )
;②a的最小值为10.则下列说法正确的是( )
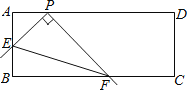
A.①②都对B.①②都错C.①对②错D.①错②对
查看答案和解析>>
科目:初中数学 来源: 题型:
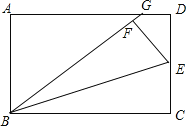
【题目】如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,将BF延长交AD于点G.若![]() ,则
,则![]() =__.
=__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com