
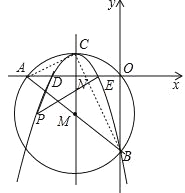
【题目】如图,在平面直角坐标系中,圆M经过原点O,直线![]() 与x轴、y轴分别相交于A,B两点.
与x轴、y轴分别相交于A,B两点.

(1)求出A,B两点的坐标;
(2)若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交![]() 轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=
轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=![]() S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)A(﹣8,0),B(0,﹣6);(2)![]() ;(3)存在.P点坐标为(﹣4+
;(3)存在.P点坐标为(﹣4+![]() ,-1)或(﹣4﹣
,-1)或(﹣4﹣![]() ,-1)或(﹣4+
,-1)或(﹣4+![]() ,1)或(﹣4﹣
,1)或(﹣4﹣![]() ,1)时,使得
,1)时,使得![]() .
.
【解析】分析:(1)令已知的直线的解析式中x=0,可求出B点坐标,令y=0,可求出A点坐标;(2)根据A、B的坐标易得到M点坐标,若抛物线的顶点C在⊙M上,那么C点必为抛物线对称轴与⊙O的交点;根据A、B的坐标可求出AB的长,进而可得到⊙M的半径及C点的坐标,再用待定系数法求解即可;
(3)在(2)中已经求得了C点坐标,即可得到AC、BC的长;由圆周角定理:
∠ ACB=90°,所以此题可根据两直角三角形的对应直角边的不同来求出不同的P点坐标.
本题解析:(1)对于直线![]() ,当
,当![]() 时,
时, ![]() ;当
;当![]() 时,
时,
所以A(﹣8,0),B(0,﹣6);
(2)在Rt△AOB中,AB=![]() =10,∵∠AOB=90°,∴AB为⊙M的直径,
=10,∵∠AOB=90°,∴AB为⊙M的直径,
∴点M为AB的中点,M(﹣4,﹣3),∵MC∥y轴,MC=5,∴C(﹣4,2),
设抛物线的解析式为y=a(x+4)+2,
把B(0,﹣6)代入得16a+2=﹣6,解得a=![]() ,
,
∴抛物线的解析式为![]() ,即
,即![]() ;
;
(3)存在.
当y=0时, ![]() ,解得x,=﹣2,x,=﹣6,
,解得x,=﹣2,x,=﹣6,
∴D(﹣6,0),E(﹣2,0),
![]() ,
,
设P(t, ![]() -6),
-6),
∵![]()
∴![]() =
=![]() 20,
20,
即|![]() |=1,当
|=1,当![]() =-1,
=-1,
解得![]() ,
, ![]() ,
,
此时P点坐标为(﹣4+![]() ,-1)或(﹣4﹣
,-1)或(﹣4﹣![]() ,-1);
,-1);
当![]() 时 ,解得
时 ,解得![]() =﹣4+
=﹣4+![]() ,
, ![]() =﹣4﹣
=﹣4﹣![]() ;
;
此时P点坐标为(﹣4+![]() ,1)或(﹣4﹣
,1)或(﹣4﹣![]() ,1).
,1).
综上所述,P点坐标为(﹣4+![]() ,-1)或(﹣4﹣
,-1)或(﹣4﹣![]() ,-1)或(﹣4+
,-1)或(﹣4+![]() ,1)或(﹣4﹣
,1)或(﹣4﹣![]() ,1)时,使得
,1)时,使得![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
(1)试判断△BEC是否为等腰三角形,请说明理由?
(2)若AB=1,∠ABE=45°,求BC的长;
(3)在原图中画△FCE,使它与△BEC关于CE的中点O成中心对称,此时四边形BCFE是什么特殊平行四边形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
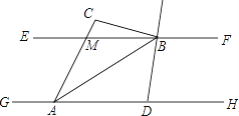
【题目】如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=100°,则∠DBA的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点O是AC与BD的交点,过点O的直线EF与AB、CD的延长线分别交于点E、F.
(1)求证:△BOE≌△DOF
(2)当EF⊥AC时,四边形AECF是怎样的特殊四边形?证明你的结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 恩施州水资源丰富,全州水能资源理论存储量为509万千瓦,可开发量349.1万千瓦,将数509万用科学记数法表示为( )
A.0.509×107B.5.09×106C.5.09×105D.5.09×102
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了考察甲、乙两种玉米的生长情况,在相同的时间,将它们种在同一块实验田里,经过一段时间后,分别抽取了10株幼苗,测得苗高如下(单位:cm):
甲:8,12,8,10,13,7,12,11,10,9;
乙:11,9,7,7,12,10,11,12,13,8.
(1)分别求出两种玉米的平均高度;
(2)哪种玉米的幼苗长得比较整齐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的盒中装着只有颜色不同的红色、黑色、白色的小球共20个,小明通过多次摸球实验后发现其中摸到红色球、黑色球的概率稳定在20%和50%,则盒子中白色球的个数很可能是_____个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com