
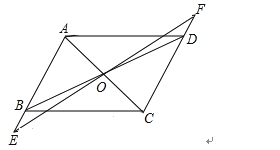
【题目】如图,在ABCD中,点O是AC与BD的交点,过点O的直线EF与AB、CD的延长线分别交于点E、F.
(1)求证:△BOE≌△DOF
(2)当EF⊥AC时,四边形AECF是怎样的特殊四边形?证明你的结论
【答案】
(1)
证明:∵四边形ABCD是矩形,
∴OB=OD,AE∥CF,
∴∠E=∠F,
在△BOE和△DOF中,
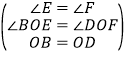 ,
,
∴△BOE≌△DOF(AAS)
(2)
解:当EF⊥AC时,四边形AECF是菱形;理由如下:如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,
又∵△BOE≌△DOF,
∴OE=OF,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF是菱形.
【解析】(1)由矩形的性质得出OB=OD,AE∥CF,得出∠E=∠F,由AAS即可证明△BOE≌△DOF;
(2)先由对角线互相平分证明四边形AECF是平行四边形,再由对角线互相垂直,即可得出结论.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分).


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】A、B两地相距216千米,甲、乙分别在A、B两地,若甲骑车的速度为15千米/时,乙骑车的速度为12千米/时。.
(1)甲、乙同时出发,背向而行,问几小时后他们相距351千米?
(2)甲、乙相向而行,甲出发三小时后乙才出发,问乙出发几小时后两人相遇?
(3)甲、乙相向而行,要使他们相遇于AB的中点,乙要比甲先出发几小时?
(4)甲、乙同时出发,相向而行,甲到达B处,乙到达A处都分别立即返回,几小时后相遇?相遇地点距离A有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商有6筐苹果,以每筐20千克为主,超过的千克数记为正数,不足的千克数记为负数,称后的记录如下:3,﹣2,2,﹣1,1,4,这6筐苹果共有多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
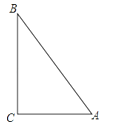
【题目】如图,点A表示小雨家,点B表示小樱家,点C表示小丽家,她们三家恰好组成一个直角三角形,其中AC⊥BC,AC=900米,BC=1200米,AB=1500米.
(1)试说出小雨家到街道BC的距离以及小樱家到街道AC的距离.
(2)画出表示小丽家到街道AB距离的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=4.固定△ABC不动,将△DEF进行如下操作:
(1)操作发现
如图①,△DEF沿线段AB向右平移(即D点在线段AB内移动),连接DC,CF,FB,四边形CDBF的形状在不断的变化,那么它的面积大小是否变化呢?如果不变化,请求出其面积.
(2)猜想论证
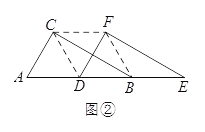
如图②,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.
(3)拓展探究
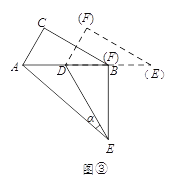
如图③,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连接AE,求sin![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,圆M经过原点O,直线![]() 与x轴、y轴分别相交于A,B两点.
与x轴、y轴分别相交于A,B两点.

(1)求出A,B两点的坐标;
(2)若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交![]() 轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=
轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=![]() S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com