
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЕуЕНжБЯпЕФОрРыМДЮЊЕуЕНжБЯпЕФДЙЯпЖЮЕФГЄЃЎ
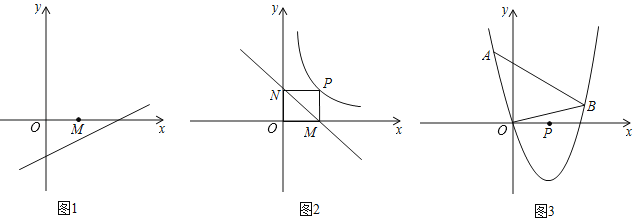
ЃЈ1ЃЉШчЭМ1ЃЌШЁЕуMЃЈ1ЃЌ0ЃЉЃЌдђЕуMЕНжБЯпlЃКyЃН![]() xЉ1ЕФОрРыЮЊЖрЩйЃП
xЉ1ЕФОрРыЮЊЖрЩйЃП
ЃЈ2ЃЉШчЭМ2ЃЌЕуPЪЧЗДБШР§КЏЪ§yЃН![]() дкЕквЛЯѓЯоЩЯЕФвЛИіЕуЃЌЙ§ЕуPЗжБ№зїPMЁЭxжсЃЌзїPNЁЭyжсЃЌМЧPЕНжБЯпMNЕФОрРыЮЊd0ЃЌЮЪЪЧЗёДцдкЕуPЃЌЪЙd0ЃН
дкЕквЛЯѓЯоЩЯЕФвЛИіЕуЃЌЙ§ЕуPЗжБ№зїPMЁЭxжсЃЌзїPNЁЭyжсЃЌМЧPЕНжБЯпMNЕФОрРыЮЊd0ЃЌЮЪЪЧЗёДцдкЕуPЃЌЪЙd0ЃН![]() ЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌШєжБЯпyЃНkx+mгыХзЮяЯпyЃНx2Љ4xЯрНЛгкxжсЩЯЗНСНЕуAЁЂBЃЈAдкBЕФзѓБпЃЉЃЎЧвЁЯAOBЃН90ЁуЃЌЧѓЕуPЃЈ2ЃЌ0ЃЉЕНжБЯпyЃНkx+mЕФОрРызюДѓЪБЃЌжБЯпyЃНkx+mЕФНтЮіЪНЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЕуPЃЈ
ЃЛЃЈ2ЃЉЕуPЃЈ![]() ЃЌ2
ЃЌ2![]() ЃЉЛђЃЈ2
ЃЉЛђЃЈ2![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉyЃНЉ2x+9
ЃЉЃЛЃЈ3ЃЉyЃНЉ2x+9
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1ЃЌЩшжБЯпlЃКyЃН![]() xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌЙ§ЕуMзїMEЁЭABЃЌЯШЧѓГіЕуAЃЌЕуBзјБъЃЌПЩЕУOAЃН2ЃЌOBЃН1ЃЌAMЃН1ЃЌгЩЙДЙЩЖЈРэПЩЧѓABГЄЃЌгЩШёНЧШ§НЧКЏЪ§ПЩЧѓНтЃЛ
xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌЙ§ЕуMзїMEЁЭABЃЌЯШЧѓГіЕуAЃЌЕуBзјБъЃЌПЩЕУOAЃН2ЃЌOBЃН1ЃЌAMЃН1ЃЌгЩЙДЙЩЖЈРэПЩЧѓABГЄЃЌгЩШёНЧШ§НЧКЏЪ§ПЩЧѓНтЃЛ
ЃЈ2ЃЉЩшЕуPЃЈaЃЌ![]() ЃЉЃЌгУВЮЪ§aБэЪОMNЕФГЄЃЌгЩУцЛ§ЙиЯЕПЩЧѓaЕФжЕЃЌМДПЩЧѓЕуPзјБъЃЛ
ЃЉЃЌгУВЮЪ§aБэЪОMNЕФГЄЃЌгЩУцЛ§ЙиЯЕПЩЧѓaЕФжЕЃЌМДПЩЧѓЕуPзјБъЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЙ§ЕуAзїACЁЭxжсгкЕуCЃЌЙ§ЕуBзїBDЁЭyжсгкЕуDЃЌЩшЕуAЃЈaЃЌa2Љ4aЃЉЃЌЕуBЃЈbЃЌb2Љ4bЃЉЃЌЭЈЙ§жЄУїЁїAOCЁзЁїBODЃЌПЩЕУabЉ4ЃЈa+bЃЉ+17ЃН0ЃЌгЩИљгыЯЕЪ§ЙиЯЕПЩЧѓa+bЃНk+4ЃЌabЃНЉmЃЌПЩЕУyЃНkx+1Љ4kЃНkЃЈxЉ4ЃЉ+1ЃЌПЩЕУжБЯпyЃНkЃЈxЉ4ЃЉ+1Й§ЖЈЕуNЃЈ4ЃЌ1ЃЉЃЌдђЕБPNЁЭжБЯпyЃНkx+mЪБЃЌЕуPЕНжБЯпyЃНkx+mЕФОрРызюДѓЃЌгЩД§ЖЈЯЕЪ§ЗЈПЩЧѓжБЯпPNЕФНтЮіЪНЃЌПЩЧѓkЃЌmЕФжЕЃЌМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌЩшжБЯпlЃКyЃН![]() xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌЙ§ЕуMзїMEЁЭABЃЌ
xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌЙ§ЕуMзїMEЁЭABЃЌ
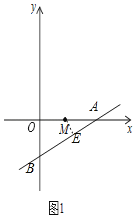
ЁпжБЯпlЃКyЃН![]() xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌ
xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌ
ЁрЕуAЃЈ2ЃЌ0ЃЉЃЌЕуBЃЈ0ЃЌЉ1ЃЉЃЌЧвЕуMЃЈ1ЃЌ0ЃЉЃЌ
ЁрAOЃН2ЃЌBOЃН1ЃЌAMЃНOMЃН1ЃЌ
ЁрABЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпtanЁЯOABЃНtanЁЯMAEЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрMEЃН![]() ЃЌ
ЃЌ
ЁрЕуMЕНжБЯпlЃКyЃН![]() xЉ1ЕФОрРыЮЊ
xЉ1ЕФОрРыЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшЕуPЃЈaЃЌ![]() ЃЉЃЌЃЈaЃО0ЃЉ
ЃЉЃЌЃЈaЃО0ЃЉ
ЁрOMЃНaЃЌONЃН![]() ЃЌ
ЃЌ
ЁрMNЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпPMЁЭxжсЃЌPNЁЭyжсЃЌЁЯMONЃН90ЁуЃЌ
ЁрЫФБпаЮPMONЪЧОиаЮЃЌ
ЁрSЁїPMNЃН![]() SОиаЮPMONЃН2ЃЌ
SОиаЮPMONЃН2ЃЌ
Ёр![]() ЁСMNЁСd0ЃН2ЃЌ
ЁСMNЁСd0ЃН2ЃЌ
Ёр![]() ЁС
ЁС![]() ЃН4ЃЌ
ЃН4ЃЌ
Ёрa4Љ10a2+16ЃН0ЃЌ
Ёрa1ЃН2ЃЌa2ЃНЉ2ЃЈЩсШЅЃЉЃЌa3ЃН2![]() ЃЌa4ЃНЉ2
ЃЌa4ЃНЉ2![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ЁрЕуPЃЈ![]() ЃЌ2
ЃЌ2![]() ЃЉЛђЃЈ2
ЃЉЛђЃЈ2![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЃЈ3ЃЉШчЭМ3ЃЌЙ§ЕуAзїACЁЭxжсгкЕуCЃЌЙ§ЕуBзїBDЁЭyжсгкЕуDЃЌ
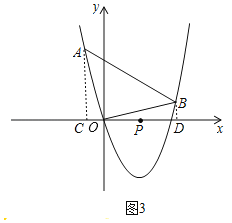
ЩшЕуAЃЈaЃЌa2Љ4aЃЉЃЌЕуBЃЈbЃЌb2Љ4bЃЉЃЌ
ЁпЁЯAOBЃН90ЁуЃЌ
ЁрЁЯAOC+ЁЯBODЃН90ЁуЃЌЧвЁЯAOC+ЁЯCAOЃН90ЁуЃЌ
ЁрЁЯBODЃНЁЯCAOЃЌЧвЁЯACOЃНЁЯBDOЃЌ
ЁрЁїAOCЁзЁїBODЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
ЁрabЉ4ЃЈa+bЃЉ+17ЃН0ЃЌ
ЁпжБЯпyЃНkx+mгыХзЮяЯпyЃНx2Љ4xЯрНЛгкxжсЩЯЗНСНЕуAЁЂBЃЌ
ЁрaЃЌbЪЧЗНГЬkx+mЃНx2Љ4xЕФСНИљЃЌ
Ёрa+bЃНk+4ЃЌabЃНЉmЃЌ
ЁрЉmЉ4ЃЈk+4ЃЉ+17ЃН0ЃЌ
ЁрmЃН1Љ4kЃЌ
ЁрyЃНkx+1Љ4kЃНkЃЈxЉ4ЃЉ+1ЃЌ
ЁржБЯпyЃНkЃЈxЉ4ЃЉ+1Й§ЖЈЕуNЃЈ4ЃЌ1ЃЉЃЌ
ЁрЕБPNЁЭжБЯпyЃНkx+mЪБЃЌЕуPЕНжБЯпyЃНkx+mЕФОрРызюДѓЃЌ
ЩшжБЯпPNЕФНтЮіЪНЮЊyЃНcx+dЃЌ
Ёр![]()
НтЕУ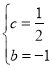
ЁржБЯпPNЕФНтЮіЪНЮЊyЃН![]() xЉ1ЃЌ
xЉ1ЃЌ
ЁрkЃНЉ2ЃЌ
ЁрmЃН1Љ4ЁСЃЈЉ2ЃЉЃН9ЃЌ
ЁржБЯпyЃНkx+mЕФНтЮіЪНЮЊyЃНЉ2x+9ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
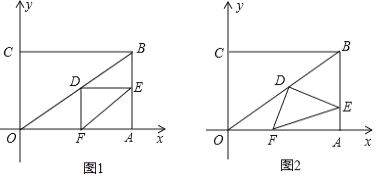
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЂйЃЌвбжЊе§ЗНаЮABCDЕФБпГЄЪЧ4ЃЌMдкDCЩЯЃЌMЪЧCDЕФжаЕуЃЌЕуPЪЧACБпЩЯЕФвЛЖЏЕуЃЌдђЕБDP+MPЕФжЕзюаЁЪБЃЌдкБИгУЭМЃЈД№ЬтОэЩЯЃЉжагУГпЙцзїГіЕуPЕФЮЛжУЃЌВЂжБНгаДГіDPЕФГЄЪЧ?
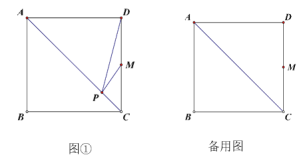
ЃЈ2ЃЉШчЭМЂкЃЌвбжЊе§ЗНаЮABCDЕФБпГЄЪЧ4ЃЌЕуMЪЧDCЩЯЕФвЛИіЖЏЕуЃЌСЌНсAMЃЌзїBPЁЭAMгкЕуPЃЌСЌНсDPЃЌЕБDPзюаЁЪБЃЌдкБИгУЭМЃЈД№ЬтОэЩЯЃЉжагУГпЙцзїГіЕуPЕФЮЛжУЃЌВЂжБНгаДГіDPЕФГЄЪЧ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
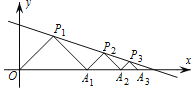
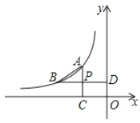
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЁїP1OA1ЃЌЁїP2A1A2ЃЌЁїP3A2A3ЁЁЖМЪЧЕШбќRtЁїЃЌжБНЧЖЅЕуP1(3ЃЌ3)ЃЌP2ЃЌP3ЁЁЃЌОљдкжБЯпyЃНЉ![]() x+4ЩЯЃЌЩшЁїP1OA1ЃЌЁїP2A1A2ЃЌЁїP3A2A3ЁЁЕФУцЛ§ЗжБ№ЮЊS1ЃЌS2ЃЌS3ЁЁдђS2019ЕФжЕЮЊЃЈ ЃЉ
x+4ЩЯЃЌЩшЁїP1OA1ЃЌЁїP2A1A2ЃЌЁїP3A2A3ЁЁЕФУцЛ§ЗжБ№ЮЊS1ЃЌS2ЃЌS3ЁЁдђS2019ЕФжЕЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁЯACBЃНЁЯDBCЃЌЬэМгвдЯТЬѕМўЃЌВЛФмХаЖЈЁїABCЁеЁїDCBЕФЪЧЃЈЁЁЁЁЃЉ
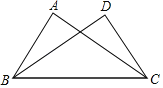
A.ЁЯABCЃНЁЯDCBB.ЁЯABDЃНЁЯDCA
C.ACЃНDBD.ABЃНDC
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌAB=6ЃЌBC=6![]() ЃЌЖЏЕуPДгЕуAГіЗЂЃЌвдУПУы
ЃЌЖЏЕуPДгЕуAГіЗЂЃЌвдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШбиЯпЖЮADдЫЖЏЃЌЖЏЕуQДгЕуDГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиелЯпЖЮDЉOЉCдЫЖЏЃЌвбжЊPЁЂQЭЌЪБПЊЪМвЦЖЏЃЌЕБЖЏЕуPЕНДяDЕуЪБЃЌPЁЂQЭЌЪБЭЃжЙдЫЖЏЃЎЩшдЫЖЏЪБМфЮЊtУыЃЎ
ИіЕЅЮЛГЄЖШЕФЫйЖШбиЯпЖЮADдЫЖЏЃЌЖЏЕуQДгЕуDГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиелЯпЖЮDЉOЉCдЫЖЏЃЌвбжЊPЁЂQЭЌЪБПЊЪМвЦЖЏЃЌЕБЖЏЕуPЕНДяDЕуЪБЃЌPЁЂQЭЌЪБЭЃжЙдЫЖЏЃЎЩшдЫЖЏЪБМфЮЊtУыЃЎ

ЃЈ1ЃЉЕБt=1УыЪБЃЌЧѓЖЏЕуPЁЂQжЎМфЕФОрРыЃЛ
ЃЈ2ЃЉШєЖЏЕуPЁЂQжЎМфЕФОрРыЮЊ4ИіЕЅЮЛГЄЖШЃЌЧѓtЕФжЕЃЛ
ЃЈ3ЃЉШєЯпЖЮPQЕФжаЕуЮЊMЃЌдкећИідЫЖЏЙ§ГЬжаЃЛжБНгаДГіЕуMдЫЖЏТЗОЖЕФГЄЖШЮЊЁЁЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕжаЃЌЙ§дЕуOМАЕуAЃЈ8ЃЌ0ЃЉЃЌCЃЈ0ЃЌ6ЃЉзїОиаЮOABCЃЌСЌНгOBЃЌЕуDЮЊOBЕФжаЕуЃЌЕуEЪЧЯпЖЮABЩЯЕФЖЏЕуЃЌСЌНгDEЃЌзїDFЁЭDEЃЌНЛOAгкЕуFЃЌСЌНгEFЃЎвбжЊЕуEДгAЕуГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдкЯпЖЮABЩЯвЦЖЏЃЌЩшвЦЖЏЪБМфЮЊtУыЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБt=3ЪБЃЌЧѓDFЕФГЄЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуEдкЯпЖЮABЩЯвЦЖЏЕФЙ§ГЬжаЃЌ![]() ЕФДѓаЁЪЧЗёЗЂЩњБфЛЏЃПШчЙћБфЛЏЃЌЧыЫЕУїРэгЩЃЛШчЙћВЛБфЃЌЧыЧѓГі
ЕФДѓаЁЪЧЗёЗЂЩњБфЛЏЃПШчЙћБфЛЏЃЌЧыЫЕУїРэгЩЃЛШчЙћВЛБфЃЌЧыЧѓГі![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ3ЃЉСЌНгADЃЌЕБADНЋЁїDEFЗжГЩЕФСНВПЗжЕФУцЛ§жЎБШЮЊ1ЃК2ЪБЃЌЧѓЯргІЕФtЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕу![]() ЁЂ
ЁЂ![]() дкЫЋЧњЯп
дкЫЋЧњЯп![]()
![]() ЩЯЃЌ
ЩЯЃЌ![]() жсгк
жсгк![]() ЃЌ
ЃЌ![]() жсгкЕу
жсгкЕу![]() ЃЌ
ЃЌ![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ
ЃЈ1ЃЉЪдХаЖЯЫФБпаЮ![]() ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ2ЃЉШє![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧѓИУЫЋЧњЯпЕФНтЮіЪНЃЎ
ЃЌЧѓИУЫЋЧњЯпЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌжБЯп
жаЃЌжБЯп![]() гыКЏЪ§
гыКЏЪ§![]() ЕФЭМЯѓНЛгк
ЕФЭМЯѓНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЧвЕу
СНЕуЃЌЧвЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉвбжЊЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїЦНаагк
зїЦНаагк![]() жсЕФжБЯпЃЌНЛжБЯп
жсЕФжБЯпЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌНЛКЏЪ§
ЃЌНЛКЏЪ§![]() ЕФЭМЯѓгкЕу
ЕФЭМЯѓгкЕу![]() ЃЎ
ЃЎ
ЂйЕБ![]() ЪБЃЌЧѓЯпЖЮ
ЪБЃЌЧѓЯпЖЮ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЂкШє![]() ЃЌНсКЯКЏЪ§ЕФЭМЯѓЃЌжБНгаДГі
ЃЌНсКЯКЏЪ§ЕФЭМЯѓЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧХзЮяЯпy1=ax2+bx+cЃЈaЁй0ЃЉЭМЯѓЕФвЛВПЗжЃЌХзЮяЯпЕФЖЅЕузјБъAЃЈ1ЃЌ3ЃЉЃЌгыxжсЕФвЛИіНЛЕуBЃЈ4ЃЌ0ЃЉЃЌжБЯпy2=mx+nЃЈmЁй0ЃЉгыХзЮяЯпНЛгкAЃЌBСНЕуЃЌЯТСаНсТлЃК
Ђй2a+b=0ЃЛЂкabcЃО0ЃЛЂлЗНГЬax2+bx+c=3гаСНИіЯрЕШЕФЪЕЪ§ИљЃЛЂмХзЮяЯпгыxжсЕФСэвЛИіНЛЕуЪЧЃЈЉ1ЃЌ0ЃЉЃЛЂнЕБ1ЃМxЃМ4ЪБЃЌгаy2ЃМy1ЃЌ
Цфжае§ШЗЕФЪЧЃЈ ЃЉ

A. ЂйЂкЂл B. ЂйЂлЂм C. ЂйЂлЂн D. ЂкЂмЂн
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com