
【题目】近来,校园安全问题引起了社会的极大关注.为了了解学生对安全知识的掌握情况,某校随机抽取了40名学生进行安全知识测试,测试成绩(百分制)如下:
78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 50
(1)本次测试属于 (填“普查”或“抽样调查”);
(2)若按如下分数段整理成绩,则表中的a= ,b= ;
成绩x | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
人数 | 1 | a | 18 | b | 3 |
(3)若用(2)中数据制作扇形统计图,求表示“70≤x<80”的扇形的圆心角度数;
(4)已知该校共有2000名学生,若规定成绩80分及以上为优秀,估计该校学生对安全知识掌握情况是优秀的有多少人?
【答案】(1)抽样调查;(2)1、17;(3)162°;(4)1000
【解析】
(1)根据普查和抽样调查的概念求解可得;
(2)由已知数据计数即可得;
(3)用360°乘70≤x<80的人数占总人数的比例可得;
(4)总人数乘以样本中80分及以上人数所占比例即可得.
解:(1)本次测试属于抽样调查,
故答案为:抽样调查;
(2)由已知数据知60≤x<70的有1人,即a=1;80≤x<90的有17人,即b=17;
故答案为:1、17;
(3)若用(2)中数据制作扇形统计图,则表示“70≤x<80”的扇形的圆心角度数360°×![]() =162°;
=162°;
(4)2000×![]() =1000(人),
=1000(人),
答:估计该校学生对安全知识掌握情况是优秀的有1000人.


科目:初中数学 来源: 题型:
【题目】一辆货车从仓库O出发在东西街道上运送水果,规定向东为正方向,一次到达的5个销售地点依次分别为A,B,C,D,E,最后回到仓库O,货车行驶的记录(单位:千米)如下:+1,+3,﹣6,﹣1,﹣2,+5.请问:
(1)请以仓库O为原点,向东为正方向,选择适当的单位长度,画出数轴,并标出A,B,C,D,E的位置;
(2)试求出该货车共行驶了多少千米?
(3)如果货车运送的水果以100千克为标准重量,超过的千克数记为正数,不足的千克数记为负数,则运往A,B,C,D,E五个地点的水果重量可记为:
+50,﹣15,+25,﹣10,﹣15,则该货车运送的水果总重量是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
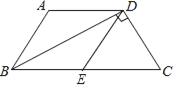
【题目】已知:如图,四边形ABCD中,AD∥BC,对角线BD平分∠ABC,且BD⊥DC,E为BC中点,AB=DE.
(1)求证:四边形ABED是菱形;
(2)若∠C=60°,CD=4,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与函数y=![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.

(1)求证:四边形DEGF是平行四边形;
(2)当点G是BC的中点时,求证:四边形DEGF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知射线OA,OB,OC,OD,∠AOD=∠BOC=α.
①若α=38°,∠COD=30°,求∠BOD、∠AOC的度数;
②若∠COD=25°,请找出图中与∠BOD相等的角,并通过计算说明理由;
(2)如图2,∠MPN是钝角,请利用三角尺画特殊角的功能,在图2中画一个与∠MPN相等的角.(标出图中特殊角的度数,并写出与∠MPN相等的角)
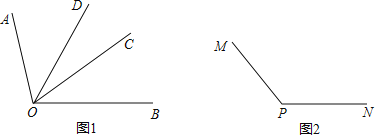
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若有理数a,b满足条件:![]() (m是整数),则称有理数a,b为一对“共享数”,其中整数m是a,b的“共享因子”.
(m是整数),则称有理数a,b为一对“共享数”,其中整数m是a,b的“共享因子”.
(1)下列两对数中:①3和5,②6和8,是一对“共享数”的是 ;(填序号)
(2)若7和x是一对“共享数”,且“共享因子”为2,求x的值;
(3)探究:当有理数a,b满足什么条件时,a,b是一对“共享数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 的两边分别平行.
的两边分别平行.
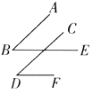
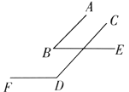
① ②
(1)在图①中,![]() 与
与![]() 的数量关系是什么?为什么?
的数量关系是什么?为什么?
(2)在图②中,![]() 与
与![]() 的数量关系是什么?为什么?
的数量关系是什么?为什么?
(3)由(1)(2)可得结论:________;
(4)应用:若两个角的两边两两互相平行,其中一个角比另一个角的2倍少![]() ,求这两个角的度数.
,求这两个角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ;直线
;直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,且点
,且点![]() 的纵坐标为4.
的纵坐标为4.

(1)不等式![]() 的解集是 ;
的解集是 ;
(2)求直线![]() 的解析式及
的解析式及![]() 的面积;
的面积;
(3)点![]() 在坐标平面内,若以
在坐标平面内,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,求符合条件的所有点
为顶点的四边形是平行四边形,求符合条件的所有点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com