
����Ŀ��ͼ�α任�е���ѧ�������龳���ڿ����ϣ���ȤѧϰС���һ����ѧ�������������̽������Rt��ABC�У���ACB��90������A��30������D��AB���е㣬����CD��̽�����֣�
��1����ͼ�٣�BC��BD��������ϵ�� ��
��2����ͼ�٣�CD��AB��������ϵ�� ����˵�����ɣ�
������֤��
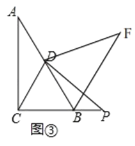
��3����ͼ�ڣ���P���߶�CB��һ���㣨��P�����B��C�غϣ�������DP�����߶�DP�Ƶ�D��ʱ����ת60�����õ��߶�DF������BF�������BF��BP��BD����֮���������ϵ����֤����Ľ��ۣ�
��չ���죺
��4������P���߶�CB�ӳ�����һ���㣬���գ�3���е�����������ͼ���в�ȫͼ��ֱ��д��BF��BP��BD����֮���������ϵ��

���𰸡���1��BC=BD����2��CD=![]() AB����3��BF+BP��BD��֤������������4����ͼ��������BF��BD+BP��
AB����3��BF+BP��BD��֤������������4����ͼ��������BF��BD+BP��
��������
��1������30��ֱ�������ε����ʺ��е�Ķ��壬���ɵõ��𰸣�
��2������30��ֱ�������ε����ʺ��е�Ķ��壬֤����DBC�ǵȱ������Σ����ɵõ��𰸣�
��3��ͬ��2���ķ����ó�BC=BD�����ó���BCD�ǵȱ������Σ������жϳ���DCP����DBF���ó�CP=BF���ɵó����ۣ�
��4��ͬ��3���ķ����ó�BC=BD�����ó���BCD�ǵȱ������Σ������жϳ���DCP�ա�DBF���ó�CP=BF���ɵó����ۣ�
�⣺��1������Rt��ABC�У���ACB��90������A��30����
��![]() ��
��
�ߵ�DʱAB���е㣬
��![]() ��
��
��BC=BD��
�ʴ�Ϊ��BC=BD��
��2��CD=![]() AB��
AB��
���ɣ��ߡ�ACB��90������A��30����
���CBA��60����BC��![]() AB��
AB��
�ߵ�D��AB���е㣬
��BC��BD��
���DBC�ǵȱ������Σ�
��CD=BC��
��BC��![]() AB��
AB��
��CD=![]() AB��
AB��
�ʴ�Ϊ��CD��![]() AB��
AB��
��3��BF+BP��BD��
���ɣ��ɣ�2��֪ ��DBC�ǵȱ������Σ�
���CDB��60����DC��DB��
���߶�DP�Ƶ�D��ʱ����ת60�����õ��߶�DF��
���PDF��60����DP��DF��
���CDB����PDB����PDF����PDB��
���CDP����BDF��
���DCP�ա�DBF��
��CP��BF��
��CP+BP��BC��
��BF+BP��BC��
��BC��BD��
��BF+BP��BD��
��4����ͼ�ۣ�BF=BD+BP��
���ɣ�����ACB=90������A=30����
���CBA=60����BC=![]() AB��
AB��
�ߵ�D��AB���е㣬
��BC=BD��
���DBC�ǵȱ������Σ�
���CDB=60����DC=DB��
���߶�DP�Ƶ�D��ʱ����ת60�����õ��߶�DF��
���PDF=60����DP=DF��
���CDB+��PDB=��PDF+��PDB��
���CDP=��BDF��
�ڡ�DCP�͡�DBF�У�
 ��
��
���DCP�ա�DBF��
��CP=BF��
��CP=BC+BP��
��BF=BC+BP��
��BC=BD��
��BF=BD+BP��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⱳ������1����ͼ![]() ����֪
����֪![]() �У�
�У�![]() ��ֱ��
��ֱ��![]() ������
������![]() ֱ��
ֱ��![]() ��
��![]() ֱ��
ֱ��![]() ������ֱ�Ϊ��
������ֱ�Ϊ��![]() ����֤��
����֤��![]() ��
��
֤����
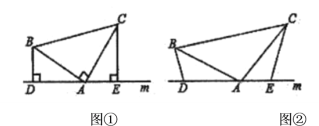
��չ���죺��2����ͼ![]() ������1���е�������Ϊ����
������1���е�������Ϊ����![]() �У�
�У�![]() ���㶼��ֱ��
���㶼��ֱ��![]() �ϣ�������
�ϣ�������![]() ����д��
����д��![]() �����߶ε�������ϵ��������Ҫ֤����
�����߶ε�������ϵ��������Ҫ֤����
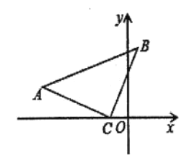
ʵ��Ӧ�ã���3����ͼ����![]() �У�
��![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ����ֱ��д����
����ֱ��д����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���������Ϊ30Ԫ��̨����40Ԫ�ļ۸��۳���ƽ��ÿ�����۳�600�������������������̨�Ƶ��ۼ�ÿ����1Ԫ���������ͼ���10�����г��涨��̨���ۼ۲��ó���60Ԫ��Ϊ��ʵ����������̨��ƽ��ÿ��10000Ԫ�����������ۼ�Ӧ��Ϊ����Ԫ����ʱ�۳�̨�ƶ��ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���B��60�㣬����C��CD��AB������ACD��60�㣬��֤����ABC�ǵȱ�������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������ۼס���������ë����֪������ë��ÿͲ���ۼ۱�������ë��ÿͲ���ۼ۶�15Ԫ��������������ĴӸ����깺����2Ͳ������ë���3Ͳ������ë������255Ԫ��
��1��������ס���������ë��ÿͲ���ۼ۸��Ƕ���Ԫ��
��2�����ݽ�����������������ߵ�������������ľ����ò�����2550ԪǮ�����ס���������ë��50Ͳ����ô�����Թ�������Ͳ������ë��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0���Ĵ���ͼ����ͼ��ʾ����������Ϊ����2����9a�������н��ۣ���4a+2b+c��0����5a��b+c=0����������a��x+5����x��1��=��1��������x1��x2����x1��x2����5��x1��x2��1����������|ax2+bx+c|=1���ĸ����������ĸ����ĺ�Ϊ��4��������ȷ�Ľ����У�������
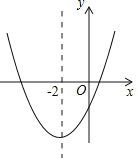
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̽���˫̨����Ϊ���˽�2016����б�ҵ����ҵ���ȥ�Բ��ֳ���ѧ�������˳������飬�ͳ���ѧ��������ȥ��A������ͨ���У�B����ְҵ����C��ֱ�ӽ�������ҵ��D����������������ͳ�ƣ���������������������ͳ��ͼ��a������b�������ʣ�
��1�����ع�������______�����б�ҵ����
��2��������ͳ��ͼ�в������IJ��ֲ���������
��3����˫̨����2016�������ҵ������4500�ˣ������˫̨��������ij�����ҵ���ж���ͨ���е�ѧ��������
��4����ʦ��Ӽס��ҡ�������4λͬѧ�����ѡ����λͬѧ�˽����DZ�ҵ���ȥ�������������״ͼ���б�����ѡ�м�ͬѧ�ĸ��ʡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧѧϰ�У���ʱ��֪ʶ���й��ɺ������Ǹ���ѧϰ����Ҫ��������ѧϰ��С����ѧϰ��һ�η��̣��飩��һԪһ�β���ʽ��һ�κ��������֪ʶ�����˹���������
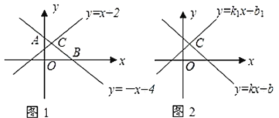
��1����������ͬһ��ƽ��ֱ������ϵ�л�����һ�κ���![]() ��
��![]() ��ͼ����ͼ��a����ʾ�������˹��ɣ�
��ͼ����ͼ��a����ʾ�������˹��ɣ�
����һ�κ����뷽�̵Ĺ�ϵ��
������һ�κ����Ľ���ʽ����һ����Ԫһ�η��̣�
��������B�ĺ������Ƿ��̢ٵĽ⣮
��������C������![]() �е�x��y��ֵ�Ƿ�����ڵĽ⣮
�е�x��y��ֵ�Ƿ�����ڵĽ⣮
����һ�κ����벻��ʽ�Ĺ�ϵ��
����������![]() �ĺ���ֵy����0ʱ���Ա���x��ȡֵ��Χ���Dz���ʽ�۵Ľ⼯��
�ĺ���ֵy����0ʱ���Ա���x��ȡֵ��Χ���Dz���ʽ�۵Ľ⼯��
����������![]() �ĺ���ֵС��0ʱ���Ա���x��ȡֵ��Χ���Dz���ʽ�ܵĽ⼯��
�ĺ���ֵС��0ʱ���Ա���x��ȡֵ��Χ���Dz���ʽ�ܵĽ⼯��
�����ͼ��1�������Ϸ����е����ݣ�������������ź�д����Ӧ�Ľ��ۣ���________����________����________����________��
��2������֪һ�κ���![]() ��
��![]() ��ͼ����ͼ��2����ʾ�������ǵĽ���C������Ϊ
��ͼ����ͼ��2����ʾ�������ǵĽ���C������Ϊ![]() ����ô����ʽ
����ô����ʽ![]() �Ľ⼯��________��
�Ľ⼯��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶�ס�������ͬѧ��ĩ���Եijɼ�(��λ����)���£�
���� | ��ѧ | Ӣ�� | ��ʷ | ���� | ���� | |
�� | 75 | 93 | 85 | 84 | 95 | 90 |
�� | 85 | 85 | 91 | 85 | 89 | 85 |
���ݱ����е����ݣ��ش��������⣺
(1)���ܷ�Ϊ522�֣����ƽ���ɼ���__________�֣��ҵ��ܷ�Ϊ520�֣�________�ijɼ���һЩ. (������������������)
(2)��������֪![]() . ����Ϊ__________��ƫ�ƣ�(������������������)
. ����Ϊ__________��ƫ�ƣ�(������������������)
(3)����¼ȡʱ����ʷ��������Ŀ��Ȩ����0.3�������Ƴɼ�Ȩ����1������˭�ijɼ�����һЩ����˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com