
【题目】问题背景:(1)如图![]() ,已知
,已知![]() 中,
中,![]() ,直线
,直线![]() 经过点
经过点![]() 直线
直线![]() ,
,![]() 直线
直线![]() ,垂足分别为点
,垂足分别为点![]() .求证:
.求证:![]() .
.
证明:
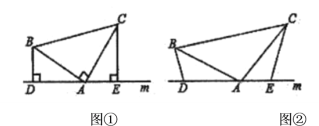
拓展延伸:(2)如图![]() ,将(1)中的条件改为:在
,将(1)中的条件改为:在![]() 中,
中,![]() 三点都在直线
三点都在直线![]() 上,并且有
上,并且有![]() .请写出
.请写出![]() 三条线段的数量关系.(不需要证明)
三条线段的数量关系.(不需要证明)
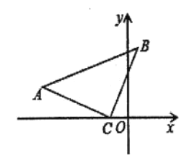
实际应用:(3)如图,在![]() 中,
中,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,请直接写出点
,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)见解析;(2)DE=BD+CE;(3)B(1,4).
【解析】
(1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA,则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;(2)利用∠BDA=∠BAC,得出∠CAE=∠ABD,进而得出△ADB≌△CEA即可得出答案.(3)过点A、B分别作x轴的垂线,垂足分别为D、E,构造(1)中的模型,进而利用(1)的结论即可求解.
(1) 证明:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
∵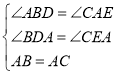 ,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2) DE=BD+CE.理由如下:
∵∠BDA=∠BAC=∠AEC,
∴∠DBA+∠BAD=∠BAD+∠CAE,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
∵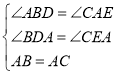 ,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(3)如图,过点A、B分别作x轴的垂线,垂足分别为D、E,
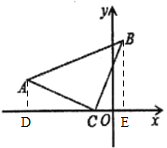
由(1)可知,AD=CE,CD=BE,
∵点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∴AD=3,CD=4,
∴OE=1,
∴点B的坐标为(1,4).


科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过![]() km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方
km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方![]() m处,过了2s后,测得小汽车与车速检测仪间距离为
m处,过了2s后,测得小汽车与车速检测仪间距离为![]() m,这辆小汽车超速了吗?
m,这辆小汽车超速了吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两张完全相同的矩形纸片![]() 、
、![]() 按如图方式放置,
按如图方式放置,![]() 为重合的对角线.重叠部分为四边形
为重合的对角线.重叠部分为四边形![]() ,
,

![]() 试判断四边形
试判断四边形![]() 为何种特殊的四边形,并说明理由;
为何种特殊的四边形,并说明理由;
![]() 若
若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
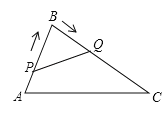
【题目】如图所示,在△ABC中,AB=8cm,BC=16 cm.点P从点A出发沿AB向点B以2 cm/s的速度运动,点Q从点B出发沿BC向点C以4 cm/s的速度运动.如果点P,Q分别从点A,B同时出发,则_____________秒钟后△PBQ与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,∠BAD=90°,对角线BD⊥DC.
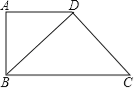
(1)△ABD与△DCB相似吗?请回答并说明理由;
(2)如果AD=4,BC=9,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为![]() .
.
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) | 10000 | ____________ |
平均步长(米/步) | 0.6 | ____________ |
距离(米) | 6000 | 7020 |
注:步数×平均步长=距离.
(1)根据题意完成表格填空;
(2)求x;
(3)王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队承包一项工程,如果甲工程队单独施工,恰好如期完成;如果乙工程队单独施工就要超过6个月才能完成,现在甲、乙两队先共同施工4个月,剩下的由乙队单独施工,则恰好如期完成.
(1)问原来规定修好这条公路需多少长时间?
(2)现要求甲、乙两个工程队都参加这项工程,但由于受到施工场地条件限制,甲、乙两工程队不能同时施工.已知甲工程队每月的施工费用为4万元,乙工程队每月的施工费用为2万元.为了结算方便,要求:甲、乙的施工时间为整数个月,不超过15个月完成.当施工费用最低时,甲、乙各施工了多少个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图![]() ,
,![]() 是
是![]() 的平分线,点
的平分线,点![]() 在
在![]() 上,
上,![]() ,且点
,且点![]() 到
到![]() 的距离为
的距离为![]() ,过点
,过点![]() 作
作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,易得到结论:
,易得到结论:![]() .
.
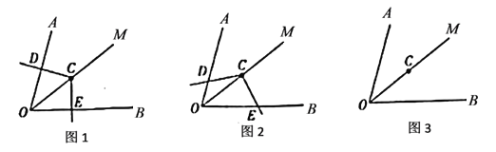
(1)把图![]() 中的
中的![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 与
与![]() 不垂直时(如图
不垂直时(如图![]() ),上述结论是否成立?并说明理由.
),上述结论是否成立?并说明理由.
(2)把图![]() 中的
中的![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 与
与![]() 的反向延长线相交于点
的反向延长线相交于点![]() 时:
时:
①请在图![]() 中画出图形;
中画出图形;
②上述结论还成立吗?若成立,请给出证明;若不成立,请直接写出线段![]() ,
,![]() 之间的的数量关系,不需证明.
之间的的数量关系,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图形变换中的数学,问题情境:在课堂上,兴趣学习小组对一道数学问题进行了深入探究,在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,连接CD.探索发现:
(1)如图①,BC与BD的数量关系是 ;
(2)如图①,CD与AB的数量关系是 ;并说明理由.
猜想验证:
(3)如图②,若P是线段CB上一动点(点P不与点B,C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想BF,BP,BD三者之间的数量关系,并证明你的结论;
拓展延伸:
(4)若点P是线段CB延长线上一动点,按照(3)中的作法,请在图③中补全图象,并直接写出BF、BP、BD三者之间的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com