
【题目】已知:如图![]() ,
,![]() 是
是![]() 的平分线,点
的平分线,点![]() 在
在![]() 上,
上,![]() ,且点
,且点![]() 到
到![]() 的距离为
的距离为![]() ,过点
,过点![]() 作
作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,易得到结论:
,易得到结论:![]() .
.
(1)把图![]() 中的
中的![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 与
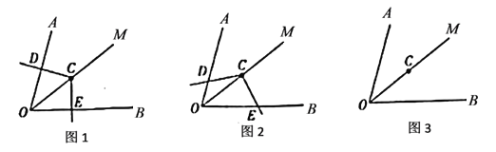
与![]() 不垂直时(如图
不垂直时(如图![]() ),上述结论是否成立?并说明理由.
),上述结论是否成立?并说明理由.
(2)把图![]() 中的
中的![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 与
与![]() 的反向延长线相交于点
的反向延长线相交于点![]() 时:
时:
①请在图![]() 中画出图形;
中画出图形;
②上述结论还成立吗?若成立,请给出证明;若不成立,请直接写出线段![]() ,
,![]() 之间的的数量关系,不需证明.
之间的的数量关系,不需证明.
【答案】8;(1)成立,理由见解析;(2)①见解析,②不成立,![]()
【解析】
先根据角平分线的性质得出![]() ,然后根据
,然后根据![]() 得出
得出![]() ,利用勾股定理即可求出OD的值,然后即可求出
,利用勾股定理即可求出OD的值,然后即可求出![]() 的值;
的值;
(1)过点![]() 作
作![]() ,
,![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,则
,则![]() ,首先证明
,首先证明![]() ,得出
,得出![]() ,然后利用勾股定理求出
,然后利用勾股定理求出![]() 的值,再证明
的值,再证明![]() ,得出
,得出![]() ,最后通过等量代换即可求出
,最后通过等量代换即可求出![]() 的值;
的值;
(2)①根据题意画出图形即可;
②过点![]() 作
作![]() ,
,![]() 交
交![]() ,
,![]() 于点
于点![]() ,
,![]() ,按照(1)的方法可得
,按照(1)的方法可得![]() ,
,![]() ,得出
,得出![]() ,
,![]() ,
,
然后通过等量代换得出![]() .
.
∵![]() 是
是![]() 的平分线,
的平分线, ![]() ,
,![]()
![]()
在![]() 和
和![]() 中,
中,![]()
![]()
![]()
![]()
![]()
![]()
(1)成立.理由:
过点![]() 作
作![]() ,
,![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,则
,则![]() ,
,

![]() 是
是![]() 的平分线,
的平分线,![]() ,
,![]()
![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,![]()
![]()
![]() ,
,
![]() ,点
,点![]() 到
到![]() 的距离为
的距离为![]() ,即
,即![]() ,
,
![]()
根据题意得,![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,
![]() ,
,
![]()
(2)①所作图形如图所示

②不成立,![]()
过点![]() 作
作![]() ,
,![]() 交
交![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,

![]() 是
是![]() 的平分线,
的平分线,![]() ,
,![]()
![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,![]()
![]()
![]() ,
,
![]() ,点
,点![]() 到
到![]() 的距离为
的距离为![]() ,即
,即![]() ,
,
![]()
根据题意得,![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
∴![]()


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,E,F,G,H分别是BD,BC,AC,AD的中点,且AB=CD,下列结论:①EG⊥FH;②四边形EFGH是菱形;③HF平分∠EHG;④EG=![]() (BC﹣AD),其中正确的个数是( )
(BC﹣AD),其中正确的个数是( )
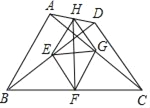
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:(1)如图![]() ,已知
,已知![]() 中,
中,![]() ,直线
,直线![]() 经过点
经过点![]() 直线
直线![]() ,
,![]() 直线
直线![]() ,垂足分别为点
,垂足分别为点![]() .求证:
.求证:![]() .
.
证明:
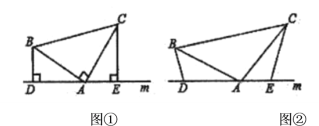
拓展延伸:(2)如图![]() ,将(1)中的条件改为:在
,将(1)中的条件改为:在![]() 中,
中,![]() 三点都在直线
三点都在直线![]() 上,并且有
上,并且有![]() .请写出
.请写出![]() 三条线段的数量关系.(不需要证明)
三条线段的数量关系.(不需要证明)
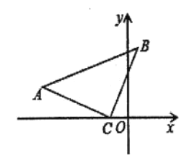
实际应用:(3)如图,在![]() 中,
中,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,请直接写出点
,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△BAD≌△EBC,∠BAD=∠BCE=90°,∠ABD=∠BEC=30°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)如图1,当A,B,E三点在同一直线上时,判断AC与CN数量关系为________;
(2)将图1中△BCE绕点B逆时针旋转到图2位置时,(1)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由;
(3)将图1中△BCE绕点B逆时针旋转一周,旋转过程中△CAN能否为等腰直角三角形?若能,直接写出旋转角度;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,点F是射线DC上一动点(不与C,D重合).连接AF并延长交直线BC于点E,交BD于H,连接CH,过点C作CG⊥HC交AE于点G.
(1)若点F在边CD上,如图1.
①证明:∠DAH=∠DCH;
②猜想:△GFC的形状并说明理由.
(2)取DF中点M,连接MG.若MG=2.5,正方形边长为4,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进货价为30元的台灯以40元的价格售出,平均每月能售出600个,经调查表明,这种台灯的售价每上涨1元,其销量就减少10个,市场规定此台灯售价不得超过60元,为了实现销售这种台灯平均每月10000元的销售利润,售价应定为多少元?这时售出台灯多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,对相关知识进行了归纳整理.
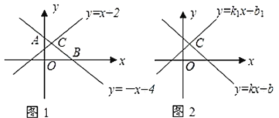
(1)例如他在同一个平面直角坐标系中画出了一次函数![]() 和
和![]() 的图像如图(a)所示,并做了归纳:
的图像如图(a)所示,并做了归纳:
(Ⅰ)一次函数与方程的关系:
(ⅰ)一次函数的解析式就是一个二元一次方程.
(ⅱ)点B的横坐标是方程①的解.
(ⅲ)点C的坐标![]() 中的x,y的值是方程组②的解.
中的x,y的值是方程组②的解.
(Ⅱ)一次函数与不等式的关系:
(ⅰ)函数![]() 的函数值y大于0时,自变量x的取值范围就是不等式③的解集.
的函数值y大于0时,自变量x的取值范围就是不等式③的解集.
(ⅱ)函数![]() 的函数值小于0时,自变量x的取值范围就是不等式④的解集.
的函数值小于0时,自变量x的取值范围就是不等式④的解集.
请根据图(1)和以上方框中的内容,在下面数字序号后写出相应的结论:①________;②________;③________;④________;
(2)若已知一次函数![]() 和
和![]() 的图像,如图(2)所示,且它们的交点C的坐标为
的图像,如图(2)所示,且它们的交点C的坐标为![]() ,那么不等式
,那么不等式![]() 的解集是________.
的解集是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com