【题目】如图，
，
为五边形
的对角线，
，
，
，
，
，若四边形
的面积为36，则
__________．
【答案】
【解析】
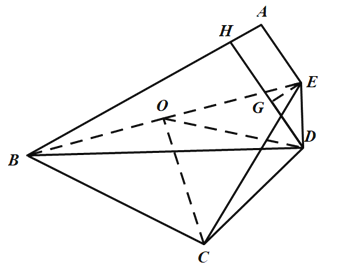
过点D作
于点H，过点E作
于点G，连接BE,取BE的中点O，连接OD,OC，先利用全等三角形的性质和角平分线的定义得出
，然后利用角度之间的计算和直角三角形的性质，三角形外角的性质得出
为等边三角形，进而得出
，然后接着证明四边形AHGE是矩形，得出
，设
利用四边形ABCE面积和HD的长度得到两个关于x,y的方程，联立即可解出x,y的值，然后求出
，最后利用即可求BC的长度．
过点D作于点H，过点E作于点G，连接BE,取BE的中点O，连接OD,OC
在
和
中，
,
为等边三角形
∵， ，
∴四边形AHGE是矩形，
设
则四边形ABCE的面积为
∴
又
∵
解得
解得
故答案为：．
同步练习强化拓展系列答案科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD，BE.
（1）求证：CE＝AD；
（2）当D为AB中点时，四边形BECD是什么特殊四边形？说明你的理由；
（3）若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某日王老师佩戴运动手环进行快走锻炼，两次锻炼后数据如表．与第一次锻炼相比，王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍．设王老师第二次锻炼时平均步长减少的百分率为
．
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) | 10000 | ____________ |
平均步长(米/步) | 0.6 | ____________ |
距离(米) | 6000 | 7020 |
注：步数×平均步长＝距离．
(1)根据题意完成表格填空；
(2)求x；
(3)王老师发现好友中步数排名第一为24000步，因此在两次锻炼结束后又走了500米，使得总步数恰好为24000步，求王老师这500米的平均步长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在菱形ABCD 中，点E，O，F分别是边AB，AC，AD的中点，连接CE、CF、OE、OF．
（1）求证：△BCE≌△DCF；
（2）当AB与BC满足什么条件时，四边形AEOF正方形？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图
，
是
的平分线，点
在上，
，且点到
的距离为
，过点作
，
，垂足分别为
，
，易得到结论：
．
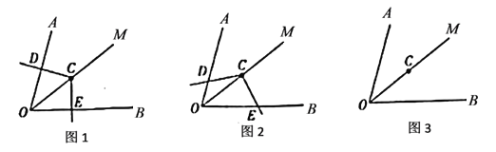
（1）把图中的
绕点旋转，当
与不垂直时（如图
），上述结论是否成立？并说明理由．
（2）把图中的绕点旋转，当与的反向延长线相交于点时：
①请在图中画出图形；
②上述结论还成立吗？若成立，请给出证明；若不成立，请直接写出线段
，
之间的的数量关系，不需证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知平面直角坐标系中，△ABC的三个顶点的坐标分别为A（2，2），B（1，﹣1），C（3，0）．
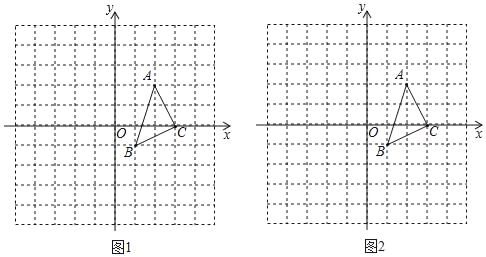
（1）在图1中，画出以点O为位似中心，放大△ABC到原来的2倍的△A1B1C1；
（2）若P（a，b）是AB边上一点，平移△ABC之后，点P的对应点P'的坐标是（a+3，b﹣2），在图2中画出平移后的△A2B2C2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在Rt△ABC中，∠ACB＝90°，AC＝10cm，BC＝5cm，点P从点C出发沿线段CA以每秒2cm的速度运动，同时点Q从点B出发沿线段BC以每秒1cm的速度运动．设运动时间为t秒（0＜t＜5）．
（1）填空：AB＝ cm；
（2）t为何值时，△PCQ与△ACB相似；
（3）如图2，以PQ为斜边在异于点C的一侧作Rt△PEQ，且
，连结CE，求CE．（用t的代数式表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算：（1）|﹣3|+（2018﹣π）0﹣
+（
）﹣1
（2）化简：（a+1）2﹣a（a﹣2）
（3）解方程：x2+4x﹣5=0；
（4）2x2﹣3x﹣1=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
