
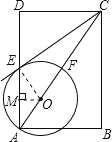
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.

【答案】(1)直线CE与⊙O相切(2)![]()
【解析】试题分析:(1)连接OE.欲证直线CE与⊙O相切,只需证明∠CEO=90°,即OE⊥CE即可;
(2)在直角三角形ABC中,根据三角函数的定义可以求得AB=![]() ,然后根据勾股定理求得AC=
,然后根据勾股定理求得AC=![]() ,同理知DE=1;在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2,即(
,同理知DE=1;在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2,即(![]() -r) 2=r2+3,从而易得r的值;
-r) 2=r2+3,从而易得r的值;
试题解析:(1)直线CE与⊙O相切
理由如下:
∵四边形ABCD是矩形,
∴BC∥AD,∠ACB=∠DAC;
又∵∠ACB=∠DCE,
∴∠DAC=∠DCE;
连接OE,则∠DAC=∠AEO=∠DCE;
∵∠DCE+∠DEC=90°
∴∠AEO+∠DEC=90°
∴∠OEC=90°,即OE⊥CE.
又OE是⊙O的半径,
∴直线CE与⊙O相切.
(2)∵tan∠ACB=![]() ,BC=2,
,BC=2,
∴AB=BCtan∠ACB=![]() ,
,
∴AC=![]() ;
;
又∵∠ACB=∠DCE,
∴tan∠DCE=tan∠ACB=![]() ,
,
∴DE=DCtan∠DCE=1;
在Rt△CDE中,CE=![]() ,
,
连接OE,设⊙O的半径为r,则在Rt△COE中,CO2=OE2+CE2,即(![]() -r) 2=r2+3
-r) 2=r2+3
解得:r=![]()


科目:初中数学 来源: 题型:
【题目】超市店庆促销,某种书包原价每个x元,第一次降价打“八折”,第二次降价每个又减10元,经两次降价后售价为90元,则得到方程( )
A.0.8x﹣10=90
B.0.08x﹣10=90
C.90﹣0.8x=10
D.x﹣0.8x﹣10=90
查看答案和解析>>
科目:初中数学 来源: 题型:
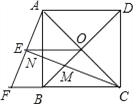
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD=![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论: ①AE=CF;
②△EPF是等腰直角三角形;
③S四边形AEPF= ![]() S△ABC;
S△ABC;
④当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合) BE+CF=EF.
上述结论中始终正确的有( )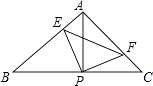
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践探究,解决问题
如图1,△ABC中,AD为BC边上的中线,则S△ABD=S△ACD . 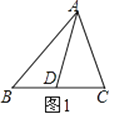
(1)在图2中,E、F分别为矩形ABCD的边AD、BC的中点,且AB=4,AD=8,则S阴影=;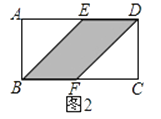
(2)在图3中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴影和S平行四边形ABCD之间满足的关系式为;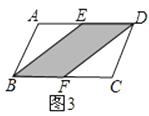
(3)在图4中,E、F分别为任意四边形ABCD的边AD、BC的中点,则S阴影和S四边形ABCD之间还满足(2)中的关系式吗?若满足,请予以证明,若不满足,说明理由.
解决问题: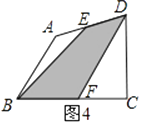
(4)在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和(即S1+S2+S3+S4的值).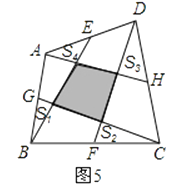
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知M,N表示单项式,且3x(M-5x)=6x2y3+N,则( )
A. M=2xy3,N=-15x B. M=3xy3,N=-15x2
C. M=2xy3,N=-15x2 D. M=2xy3,N=15x2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com