
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论: ①AE=CF;
②△EPF是等腰直角三角形;
③S四边形AEPF= ![]() S△ABC;
S△ABC;
④当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合) BE+CF=EF.
上述结论中始终正确的有( )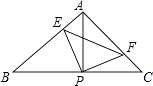
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:∵∠APE、∠CPF都是∠APF的余角, ∴∠APE=∠CPF,
∵AB=AC,∠BAC=90°,P是BC中点,
∴AP=CP,
又∵AP=CP,∠EPA=∠FPC,∠EAP=∠FCP=45°
∴△APE≌△CPF(ASA),同理可证△APF≌△BPE,
∴AE=CF,△EPF是等腰直角三角形,S四边形AEPF= ![]() S△ABC , ①②③正确;
S△ABC , ①②③正确;
故AE=FC,BE=AF,
∴AF+AE>EF,
∴BE+CF>EF,故④不成立.
始终正确的是①②③.故选C.
【考点精析】通过灵活运用等腰直角三角形和旋转的性质,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
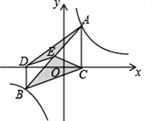
【题目】如图,点A,B在反比例函数![]() (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,﹣1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标,并画出△A1B1C1 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层… 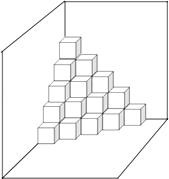
(1)第三层有个小正方体.
(2)从第四层至第六层(含第四层和第六层)共有个小正方体.
(3)第n层有个小正方体.
(4)若每个小正方体边长为a分米,共摆放了n层,则要将摆放的小正方体能看到的表面部分涂上防锈漆,则防锈漆的总面积为分米2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各项调查,适合抽样调查的是( )
①调查中央电视台《焦点访谈》节目的收视率;②某班学生订制校服,对学生胸围、腰围进行测量;③一批罐头产品的质量检验;④对河水污染情况的调查.
A. ①②B. ②③④C. ①③④D. ①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com