
【题目】已知某种月饼形状的俯视图如图1所示,该形状由1个正六边形和6个半圆组成,半圆直径与正六边形的边长相等.

现商家设计了2种棱柱体包装盒,其底面分别为矩形和正六边形(如图2和图3)我们可从底面的利用率来记算整个包装盒的利用情况.(底面利用率=![]() ×100%)
×100%)

(1)请分别计算出图2与图3中的底面利用率(结果保留到0.1%);
(2)考虑到节约成本,商家希望底面利用率能够不低于80%,且底面图形仍然采用最基本的几何形状,请问商家的要求是否能够满足,若可以满足,请设计一种方案,并直接写出此时的利用率;若不能满足,请说明理由.
【答案】(1)图2、3的底面利用率分别约为66.4%、40.2%;(2)设计底面为圆形的包装盒,利用率约为84.5%.
【解析】
(1)设半圆直径与正六边形的边长为a,根据正多边形和圆的知识,算出月饼面积,再算出图2正方形的边长,即可求出图2的面积,和图2底面的利用率;图3的包装盒六边形和月饼相似,利用面积比等于相似比的平方,求出图3包装盒的底面利用率;
(2)设计底面为圆形的包装盒,求出其半径、面积、底面利用率,满足底面利用率不低于80%.
解:(1)设半圆直径与正六边形的边长![]() a,连接正六边形的中心
a,连接正六边形的中心![]() 和两相邻的顶点
和两相邻的顶点![]() ,则
,则![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() =a,
=a,
过点![]() 作
作![]() ,
,
∴![]() ,
,![]()
![]() ,
,
∴![]()
![]() =
=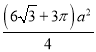 ,
,
延长OC与其中一个半圆交于点D,
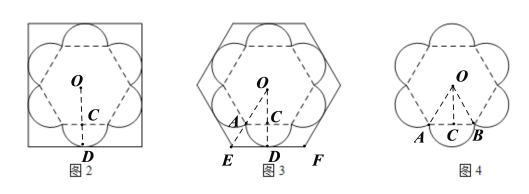
则![]()
![]()
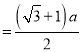 ,
,
∴![]()
![]() ,
,
![]()
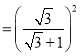
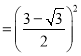
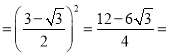
![]()
![]() 40.2%;
40.2%;
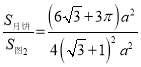 =
=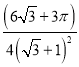 =
=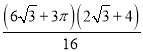 =
=![]()
![]() 66.4%;
66.4%;
答:图2、3的底面利用率分别约为66.4%、40.2%;
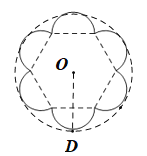
(2)商家的要求是否能够满足,设计如图所示底面为圆的包装盒,半径为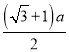 ,
,
![]()
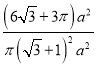 =
=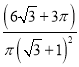
![]()
![]() ,
,
答:设计底面为圆形的包装盒,利用率约为84.5%.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,中线BE、CF相交于点G,连接EF,下列结论:
①![]() =
=![]() ; ②
; ②![]() =
=![]() ; ③
; ③![]() =
=![]() ; ④
; ④![]() =
=![]() .其中正确的个数有( )
.其中正确的个数有( )
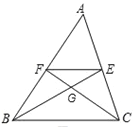
A. 1个 B. C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
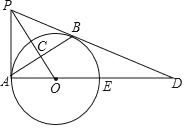
【题目】如图,PB与⊙O相切于点B,过点B作OP的垂线BA,垂足为C,交⊙O于点A,连结PA,AO,AO的延长线交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若tan∠BAD=![]() , 且OC=4,求PB的长.
, 且OC=4,求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(b≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(﹣1,0),下面的四个结论:①OA=3 ②a+b+c<0 ③ac>0 ④当y>0时,﹣1<x<3,其中正确的结论是( )
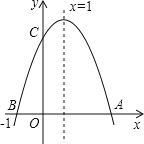
A.②④B.①③C.①④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明与小亮两个人打算骑共享单车骑行出游,两人打开手机APP进行选择,已知附近共有3种品牌的5辆车,其中A品牌与B品牌各有2辆,C品牌有1辆,手机上无法识别品牌,且有人选中车后其他人无法再选.
(1)若小明首先选择,则小明选中A品牌单车的概率为 ;
(2)求小明和小亮选中同一品牌单车的概率.(请用“画树状图”或“列表”的方法给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与坐标轴分别交于A,B,C,点D在x轴上,AC=CD,过点D作DE⊥x轴交抛物线于点E,点P,Q分别是线段CO,CD上的动点,且CP=QD.记△APC的面积为S1,△PCQ的面积为S2,△QED的面积为S3,
与坐标轴分别交于A,B,C,点D在x轴上,AC=CD,过点D作DE⊥x轴交抛物线于点E,点P,Q分别是线段CO,CD上的动点,且CP=QD.记△APC的面积为S1,△PCQ的面积为S2,△QED的面积为S3,
(1)若S1+S3=4S2 ,求Q点坐标;
(2)连结AQ,求AP+AQ的最小值;
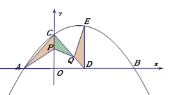
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() ,
,![]() 为常数,
为常数,![]() )的图象记为L.
)的图象记为L.
(1)若![]() =1,
=1,![]() =3,求图象L的顶点坐标;
=3,求图象L的顶点坐标;
(2)若图象L过点(4,1),且2≤a≤5,求![]() 的最大值;
的最大值;
(3)若![]() ,点
,点![]() ,
,![]() 在图象L上,当
在图象L上,当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
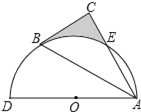
【题目】如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B、E是半圆弧的三等分点,弧BE的长为![]() π,则图中阴影部分的面积为( )
π,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
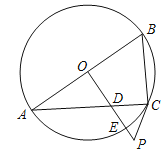
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.
(1)求证:PC是⊙O的切线;
(2)若∠P=60°,PC=2,求PE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com