
【题目】如图,在△ABC中,中线BE、CF相交于点G,连接EF,下列结论:
①![]() =
=![]() ; ②
; ②![]() =
=![]() ; ③
; ③![]() =
=![]() ; ④
; ④![]() =
=![]() .其中正确的个数有( )
.其中正确的个数有( )
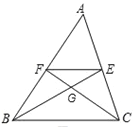
A. 1个 B. C. 3个 D. 4个
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】已知:正方形![]() 中,
中,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() (或它们的延长线)于点
(或它们的延长线)于点![]() .
.
当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图1),易证
时(如图1),易证![]() .
.
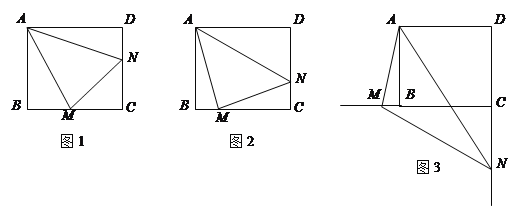
(1)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图2),线段
时(如图2),线段![]() 和
和![]() 之间有怎样的数量关系?写出猜想,并加以证明.
之间有怎样的数量关系?写出猜想,并加以证明.
(2)当![]() 绕点
绕点![]() 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段![]() 和
和![]() 之间又有怎样的数量关系?请直接写出你的猜想.
之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为![]() 元(
元(![]() 为正整数),每月的销售量为
为正整数),每月的销售量为![]() 条.
条.
(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设该网店每月获得的利润为![]() 元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣(x﹣1)2+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,CD∥x轴交抛物线于另一点D,连结AC,DE∥AC交边CB于点E.
(1)求A,B两点的坐标;
(2)求△CDE与△BAC的面积之比.
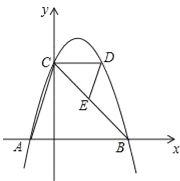
查看答案和解析>>
科目:初中数学 来源: 题型:
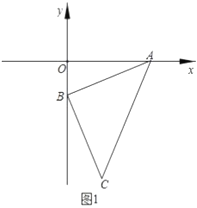
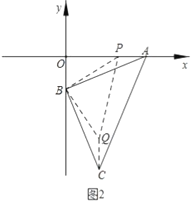
【题目】如图,已知![]() ,
,![]() ,连接
,连接![]() ,过
,过![]() 点作
点作![]() 的垂线段
的垂线段![]() ,使
,使![]() ,连接
,连接![]() .
.
(1)如图1,求![]() 点坐标;
点坐标;
(2)如图2,若![]() 点从
点从![]() 点出发沿
点出发沿![]() 轴向左平移,连接
轴向左平移,连接![]() ,作等腰直角
,作等腰直角![]() ,连接
,连接![]() ,当点
,当点![]() 在线段
在线段![]() 上,求证:
上,求证:![]() ;
;
(3)在(2)的条件下若![]() 、
、![]() 、
、![]() 三点共线,求此时
三点共线,求此时![]() 的度数及
的度数及![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:有这样一个问题:关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的且非零的实数根探究
有两个不相等的且非零的实数根探究![]() ,
,![]() ,
,![]() 满足的条件.
满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:①设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
②借助二次函数图象,可以得到相应的一元二次中![]() ,
,![]() ,
,![]() 满足的条件,列表如下:
满足的条件,列表如下:
方程根的几何意义:
方程两根的情况 | 对应的二次函数的大致图象 |
|
方程有两个不相等的负实根 |
|
|
____________ |
|
|
方程有两个不相等的正实根 | ____________ | ____________ |
(1)参考小明的做法,把上述表格补充完整;
(2)若一元二次方程![]() 有一个负实根,一个正实根,且负实根大于-1,求实数
有一个负实根,一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种月饼形状的俯视图如图1所示,该形状由1个正六边形和6个半圆组成,半圆直径与正六边形的边长相等.

现商家设计了2种棱柱体包装盒,其底面分别为矩形和正六边形(如图2和图3)我们可从底面的利用率来记算整个包装盒的利用情况.(底面利用率=![]() ×100%)
×100%)

(1)请分别计算出图2与图3中的底面利用率(结果保留到0.1%);
(2)考虑到节约成本,商家希望底面利用率能够不低于80%,且底面图形仍然采用最基本的几何形状,请问商家的要求是否能够满足,若可以满足,请设计一种方案,并直接写出此时的利用率;若不能满足,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com