
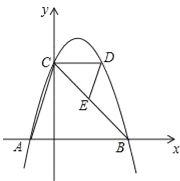
【题目】如图,抛物线y=﹣(x﹣1)2+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,CD∥x轴交抛物线于另一点D,连结AC,DE∥AC交边CB于点E.
(1)求A,B两点的坐标;
(2)求△CDE与△BAC的面积之比.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
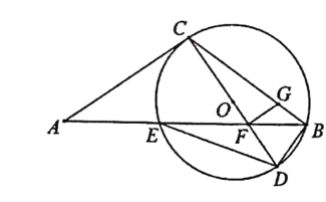
【题目】已知:△ABC内接于⊙O,连接CO并延长交AB于点E,交⊙O于点D,满足∠BEC=3∠ACD.
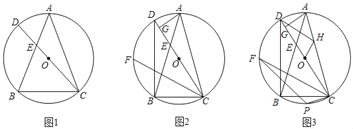
(1)如图1,求证:AB=AC;
(2)如图2,连接BD,点F为弧BD上一点,连接CF,弧CF=弧BD,过点A作AG⊥CD,垂足为点G,求证:CF+DG=CG;
(3)如图3,在(2)的条件下,点H为AC上一点,分别连接DH,OH,OH⊥DH,过点C作CP⊥AC,交⊙O于点P,OH:CP=1:![]() ,CF=12,连接PF,求PF的长.
,CF=12,连接PF,求PF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
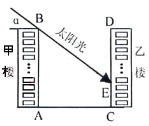
【题目】下图为某小区的两幢1O层住宅楼,由地面向上依次为第1层、第2层、…、第10层,每层的高度为3m,两楼间的距离AC=30m.现需了解在某一时段内,甲楼对乙楼的采光的影响情况.假设某一时刻甲楼楼顶B落在乙楼的影子长EC=h,太阳光线与水平线的夹角为α.
(1)用含α的式子表示h;
(2)当α=30°时,甲楼楼顶B的影子落在乙楼的第几层?从此时算起,若α每小时增加10°,几小时后,甲楼的影子刚好不影响乙楼采光.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在△ABC的边AB上,过点B,C,E的⊙O切AC于点C.直径CD交BE于点F,连结BD,DE.已知∠A=∠CDE,AC=2![]() ,BD=1.
,BD=1.
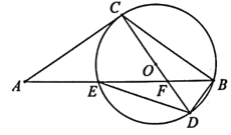
(1)求⊙O的直径.
(2)过点F作FG⊥CD交BC于点G,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断正确的是( )
A. “任意选择某一电视频道,它正在播放动画片”是必然事件
B. 某运动员投一次篮,投中的概率为0.8,则该运动员投5次篮,一定有4次投中
C. 任意抛掷一枚均匀的硬币,反面朝上的概率为![]()
D. 布袋里有3个白球,1个黑球.任意取出1个球,恰好是黑球的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
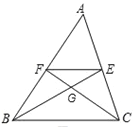
【题目】如图,在△ABC中,中线BE、CF相交于点G,连接EF,下列结论:
①![]() =
=![]() ; ②
; ②![]() =
=![]() ; ③
; ③![]() =
=![]() ; ④
; ④![]() =
=![]() .其中正确的个数有( )
.其中正确的个数有( )
A. 1个 B. C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
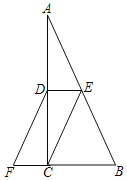
【题目】如图,在△ABC中,∠ACB=90°,点D、E分别是AC、AB的中点,点F在BC的延长线上,且∠CDF=∠A.
(1)求证:四边形DECF是平行四边形;
(2)若∠A=30°,写出图中所有与FD长度相等的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
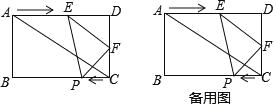
【题目】如图,在矩形 ABCD 中,AB=6cm,AD=8cm,直线 EF 从点 A 出发沿 AD 方向匀速运动,速度是 2cm/s,运动过程中始终保持 EF∥AC.F 交
AD 于 E,交 DC 于点 F;同时,点 P 从点 C 出发沿 CB 方向匀速运动,速度是 1cm/s,连接 PE、PF,设运动时间 t(s)(0<t<4).
(1)当 t=1 时,求 EF 长;
(2)求 t 为何值时,四边形 EPCD 为矩形;
(3)设△PEF 的面积为 S(cm2),求出面积 S 关于时间 t 的表达式;
(4)在运动过程中,是否存在某一时刻使 S△PC F:S 矩形 ABCD=3:16?若存在, 求出 t 的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明与小亮两个人打算骑共享单车骑行出游,两人打开手机APP进行选择,已知附近共有3种品牌的5辆车,其中A品牌与B品牌各有2辆,C品牌有1辆,手机上无法识别品牌,且有人选中车后其他人无法再选.
(1)若小明首先选择,则小明选中A品牌单车的概率为 ;
(2)求小明和小亮选中同一品牌单车的概率.(请用“画树状图”或“列表”的方法给出分析过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com