练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，下列推理所注理由正确的是（　　）

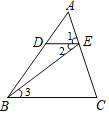
    A.∵DE∥BC，∴∠1＝∠C（同位角相等，两直线平行）

    B.∵∠2＝∠3，∴DE∥BC（两直线平行，内错角相等）

    C.∵DE∥BC，∴∠2＝∠3（两直线平行，内错角相等）

    D.∵∠DEC+∠C＝180°，∴DE∥BC（同旁内角相等，两直线平行）

    【答案】C

    【解析】

    根据平行线的判定定理以及性质逐项判断即可．

    解：A、∵DE∥BC，∴∠1＝∠C（同位角相等，两直线平行），应为：两直线平行，同位角相等，故错误；

    B、∵∠2＝∠3，∴DE∥BC（两直线平行，内错角相等），应为：内错角相等，两直线平行，故错误；

    C、∵DE∥BC，∴∠2＝∠3（两直线平行，内错角相等），正确；

    D、∵∠DEC+∠C＝180°，∴DE∥BC（同旁内角相等，两直线平行），应为：同旁内角互补，两直线平行．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知 a b ， a 与b 两个数在数轴上对应的点分别为点 A 、点 B ，求 A 、 B 两点之间的距离.

    （探索）

    小明利用绝对值的概念，结合数轴，进行探索：

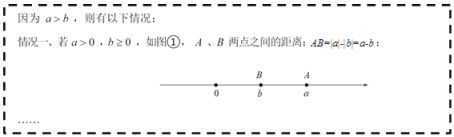
    （1）补全小明的探索

    （应用）

    （2）若点C 对应的数c ，数轴上点C 到A、B 两点的距离相等，求c .（用含a、b 的代数式表示）

    （3）若点 D对应的数 d ，数轴上点 D 到 A 的距离是点 D 到 B 的距离的nn 0 倍，请探索 n 的取值范围与点 D 个数的关系，并直接写出a、b 、d、n 的关系.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】类比学习：一动点沿着数轴向右平移3个单位，再向左平移个单位，相当于向右平移1个单位．用实数加法表示为 ．

    若坐标平面上的点作如下平移：沿轴方向平移的数量为（向右为正，向左为负，平移个单位），沿轴方向平移的数量为（向上为正，向下为负，平移个单位），则把有序数对{，}叫做这一平移的“平移量”；“平移量”{，}与“平移量”{，}的加法运算法则为．

    解决问题：（1）计算：{3，1}+{1，2}；{1，2}+{3，1}．

    （2）①动点P从坐标原点O出发，先按照“平移量”{3，1}平移到A，再按照“平移量”{1，2}平移到B；若先把动点P按照“平移量”{1，2}平移到C，再按照“平移量”{3，1}平移，最后的位置还是点B吗？在图中画出四边形OABC.

    ②证明四边形OABC是平行四边形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】10袋小麦称重后记录如下（单位：kg）.88.8，91，91.5，89，91.2，91.3，88.9，91.2，91，91.1．

    （1）如果每袋小麦以90 kg为标准，超过的千克数记作正数，不足的千克数记作负数，这10袋小麦总计超过多少千克或不足多少千克？

    （2）10袋小麦一共多少千克？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学七、八年级各选派10名选手参加知识竞赛，计分采用10分制，选手得分均为整数，成绩达到6分或6分以上为合格，达到9分或10分为优秀．这次竞赛后，七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下，其中七年级代表队得6分、10分选手人数分别为a，b．

    （1）请依据图表中的数据，求a，b的值．

    （2）直接写出表中的m= ，n= ．

    （3）有人说七年级的合格率、优秀率均高于八年级，所以七年级队成绩比八年级队好，但也有人说八年级队成绩比七年级队好．请你给出两条支持八年级队成绩好的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠BAC＝90°，AD是高，BE是中线，CF是角平分线，CF交AD于G，交BE于H．下列结论：①S△ABE＝S△BCE；②∠AFG＝∠AGF；③∠FAG＝2∠ACF；④BH＝CH．其中所有正确结论的序号是

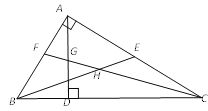
    A.①②③④B.①②③C.②④D.①③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一组数据6，3，4，7，6，3，5，6，求：

    （1）这组数据的平均数、众数、中位数；

    （2）这组数据的方差和标准差.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】5月23、24日，兰州市九年级学生进行了中考体育测试，某校抽取了部分学生的一分钟跳绳测试成绩，将测试成绩整理后作出如统计图．甲同学计算出前两组的频率和是0．12，乙同学计算出第一组的频率为0.04，丙同学计算出从左至右第二、三、四组的频数比为4：17：15．结合统计图回答下列问题：

    (1)这次共抽取了多少名学生的一分钟跳绳测试成绩？

    (2)若跳绳次数不少于130次为优秀，则这次测试成绩的优秀率是多少？

    (3)如果这次测试成绩中的中位数是120次，那么这次测试中，成绩为120次的学生至少有多少人？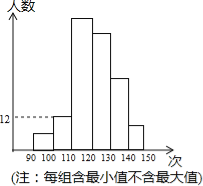

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料并解决有关问题：

    我们知道：|x|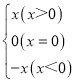＝，现在我们可以用这一结论来化简含有绝对值的代数式，如化简代数式|x+1|+|x﹣2|时，可令x+1＝0和x﹣2＝0，分别求得x＝﹣1，x＝2（称﹣1，2分别为|x+1|与|x﹣2|的零点值）．在实数范围内，零点值x＝﹣1和x＝2可将全体实数分成不重复且不遗漏的如下3种情况：①x＜﹣1；②﹣1≤x＜2；③x≥2．

    从而化简代数式|x+1|+|x﹣2|可分以下3种情况：

    ①当x＜﹣1时，原式＝﹣（x+1）﹣（x﹣2）＝﹣2x+1；

    ②当﹣1≤x＜2时，原式＝x+1﹣（x﹣2）＝3；

    ③当x≥2时，原式＝x+1+x﹣2＝2x﹣1；

    综上讨论，原式＝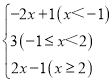

    通过以上阅读，请你解决以下问题：

    （1）当x＜2时，|x﹣2|＝　 　；

    （2）根据材料中的方法化简代数式|x+2|+|x﹣4|；（写出解答过程）

    （3）直接写出|x﹣1|﹣4|x+1|的最大值　 　．

    查看答案和解析>>

    同步练习册答案