
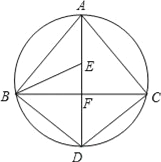
【题目】如图,⊙O 的半径为1,直线CD 经过圆心O,交⊙O 于C、D 两点,直径AB⊥CD,点 M 是直线CD 上异于点C、O、D 的一个动点,AM 所在的直线交⊙O 于点N,点 P 是直线CD 上另一点,且PM=PN.

(1)当点 M 在⊙O 内部,如图①,试判断 PN 与⊙O 的关系,并写出证明过程;
(2)当点 M 在⊙O 外部,如图②,其他条件不变时,(1)的结论是否还成立? 请说明理由;
(3)当点 M 在⊙O 外部,如图③,∠AMO=15°,求图中阴影部分的面积.
【答案】(1)详见解析;(2)成立,理由详见解析;(3)![]() +
+![]() -
-![]() .
.
【解析】试题分析:(1)PN 与⊙O 相切.要证明ON![]() PN即可,连接ON,PM=PN,所以∠PNM=∠PMN,∠AMO=∠PMN,AB⊥CD,所以∠PMN+∠MAO=90°,又因∠MAO=∠MNO,所以∠PNM+∠MNO=90°,所以PN 与⊙O 相切.(2)成立,进行等量代换,∠MAO+∠OMA=90°,因∠OMA=∠PNM,∠MAO=∠ONA,所以∠PNM+∠ONA=90°,所以∠ONP=90°;(3)阴影部分的面积可通过S
PN即可,连接ON,PM=PN,所以∠PNM=∠PMN,∠AMO=∠PMN,AB⊥CD,所以∠PMN+∠MAO=90°,又因∠MAO=∠MNO,所以∠PNM+∠MNO=90°,所以PN 与⊙O 相切.(2)成立,进行等量代换,∠MAO+∠OMA=90°,因∠OMA=∠PNM,∠MAO=∠ONA,所以∠PNM+∠ONA=90°,所以∠ONP=90°;(3)阴影部分的面积可通过S![]() AOC+S扇形AOC-S
AOC+S扇形AOC-S![]() AON求得.
AON求得.
(1)PN 与⊙O 相切.证明:连接ON,则∠ONA=∠OAN.
∵PM=PN,∴∠PNM=∠PMN.又∵∠AMO=∠PMN,
∴∠PNM=∠AMO.
∴∠PNO=∠PNM+∠ONA=∠AMO+∠OAN=90°,即PN 与⊙O 相切.
(2)成立.理由如下:连接ON,则∠ONA=∠OAN.
∵PM=PN,∴∠PNM=∠PMN.
在Rt△AOM中,∠OMA+∠OAM=90°.∴∠PNM+∠ONA=90°,
∴∠PNO=180°-90°=90°.即PN 与⊙O 相切.
(3)连接ON,由(2)可知∠ONP=90°.
∵∠AMO=15°,PM=PN,∴∠PNM=15°,∠OPN=30°,
∴∠PON=60°,∠AON=30°.
过点N 作NE⊥OD,垂足为点E.则OE=![]() .∴NE=
.∴NE=![]() .
.
∴S阴影=S△AOC+S扇形AON-S△CON=![]() OC·OA+
OC·OA+![]() -
-![]() CO·NE
CO·NE
=![]() +
+![]() -
-![]()
∴图中阴影部分的面积为![]() +
+![]() -
-![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点C,D是半圆![]() 上的三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.则下列结论:
上的三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.则下列结论:
①∠CBA=30°,②OD⊥BC,③OE=![]() AC,④四边形AODC是菱形.
AC,④四边形AODC是菱形.
正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,甲、乙两个容器内都装了一定数量的水,现将甲容器中的水匀速倒入乙容器中. 图2中,线段AB、线段CD分别表示容器中的水的深度h(厘米)与倒入时间t(分钟)的函数图像.
(1)请说出点C的纵坐标的实际意义;
(2)经过多长时间,甲、乙两个容器中的水的深度相等?
(3)如果甲容器的底面积为10cm2,求乙容器的底面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种细胞的直径约为0.00000156米.将0.00000156用科学记数法表示应为( )
A.1.56×106B.1.56×10-6C.1.56×10-5D.15.6×10-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC⊥AC,BC=8,AC=6,AB=10,则点 C 到线段 AB 的距离是_____.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923292236627968/1924724835434496/STEM/46ca9c8351da4594816ea507a60c9cdd.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:

(1)如果∠1=∠B,那么_______∥_______,根据是__________________________;
(2)如果∠3=∠D,那么_______∥_______,根据是__________________________;
(3)如果要使BE∥DF,必须∠1=∠_______,根据是_________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句中,是真命题的是( )
A.相等的角是对顶角
B.同旁内角互补
C.过一点不只有一条直线与已知直线垂直
D.对于直线 a、b、c,如果 b∥a,c∥a,那么 b∥c
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com