
 如图,⊙O经过△ABC的三个顶点,过O与BC垂直的直线分别与AC、BC相交于D、E.若∠ABC=80°,∠C=40°,则∠EDC=50°,∠BOE=60°.
如图,⊙O经过△ABC的三个顶点,过O与BC垂直的直线分别与AC、BC相交于D、E.若∠ABC=80°,∠C=40°,则∠EDC=50°,∠BOE=60°.  课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源:2017届江苏省九年级下学期第一次月考数学试卷(解析版) 题型:判断题
如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)若直线y=kx+t经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;
(3)点P在抛物线的对称轴x=1上运动,请探索:在x轴上方是否存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切?若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省东台市第四教育联盟八年级下学期第一次月考数学试卷(解析版) 题型:填空题
在 ABCD中,若∠A+∠C =140°,那么∠D =______________.
ABCD中,若∠A+∠C =140°,那么∠D =______________.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
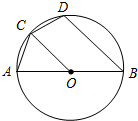 如图,AB为⊙O的直径,弦AC=CD.
如图,AB为⊙O的直径,弦AC=CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P、Q的分别从点A和点C同时出发,沿边AB,CB向终点B移动.已知点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动,设P,Q两点移动时间为xs.问是否存在这样的x,使得四边形APQC的面积等于16cm2?若存在,请求出此时x的值;若不存在,请说明理由.
如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P、Q的分别从点A和点C同时出发,沿边AB,CB向终点B移动.已知点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动,设P,Q两点移动时间为xs.问是否存在这样的x,使得四边形APQC的面积等于16cm2?若存在,请求出此时x的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 为了庆祝2016年的G20峰会在杭州举办,七年级同学在班会课进行了趣味活动.小舟同学在模板上画出一个菱形ABCD,将它以点O为中心按顺时针方向分别旋转90°、180°、270°后得到如图所示的图形,其中∠ABC=120°,AB=10cm.然后小舟将此图形制作成一个靶子,那么当我们投飞镖时命中阴影部分的概率为( )
为了庆祝2016年的G20峰会在杭州举办,七年级同学在班会课进行了趣味活动.小舟同学在模板上画出一个菱形ABCD,将它以点O为中心按顺时针方向分别旋转90°、180°、270°后得到如图所示的图形,其中∠ABC=120°,AB=10cm.然后小舟将此图形制作成一个靶子,那么当我们投飞镖时命中阴影部分的概率为( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $2-\sqrt{3}$ | C. | $\sqrt{3}-1$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com