练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

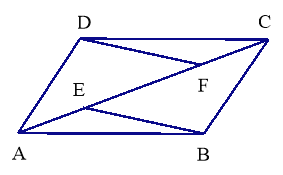
    【题目】已知：如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF.

    求证：（1）△ABE≌△CDF；（2）BE∥DF．

    【答案】(1)、证明过程见解析；(2)、证明过程见解析.

    【解析】

    试题分析：(1)、根据平行四边形得出AB=CD，AB∥CD，即∠ABE=∠DCF，结合AE=CF得出△ABE和△DCF全等；(2)、根据全等得出∠AEB=∠CFD，从而得到∠BEC=∠AFD，得到平行.

    试题解析：(1)、∵四边形ABCD是平行四边形 ∴AB=CD，AB∥CD ∴∠BAE=∠DCF

    又∵AE=CF ∴△ABE≌△DCF(SAS)

    (2)、由（1）知△ABE≌△DCF ∴∠AEB=∠CFD ∵∠AEB+∠CEB=∠CFD+∠AFD=180°

    ∴∠BEC=∠AFD ∴BE∥DF.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（2011贵州安顺，10，3分）一只跳蚤在第一象限及x轴、y轴上跳动，在第一秒钟，它从原点跳动到(0，1)，然后接着按图中箭头所示方向跳动[即(0，0)→(0，1) →(1，1) →（1，0）→…]，且每秒跳动一个单位，那么第35秒时跳蚤所在位置的坐标是（ ）

    A. (4，O) B. (5，0) C. (0，5) D. (5，5)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c的图象如图所示，给出下列结论：①abc＞0；②a﹣b+c＜0；③2a+b﹣c＜0；④4a+2b+c＞0，⑤若点（﹣ ，y1）和（ ，y2）在该图象上，则y1＞y2 ． 其中正确的结论是（填入正确结论的序号）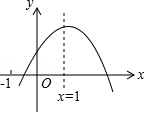

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，若∠A=15°，AB=BC=CD=DE=EF，则∠DEF等于__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

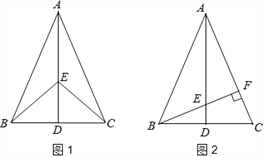
    【题目】如图1，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．

    （1）求证：BE=CE；

    （2）如图2，若BE的延长线交AC于点F，且BF⊥AC，垂足为F，∠BAC=45°，原题设其它条件不变．求证：△AEF≌△BCF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我国实施的“一带一路”战略方针，惠及沿途各国．中欧班列也已融入其中．从我国重庆开往德国的杜伊斯堡班列，全程约11025千米．同样的货物，若用轮船运输，水路路程是铁路路程的1.6倍，水路所用天数是铁路所用天数的3倍，列车平均日速（平均每日行驶的千米数）是轮船平均日速的2倍少49千米．分别求出列车及轮船的平均日速．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠BAC=45°，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，且EH=EB.下列四个结论：①∠ABC=45°；②AH=BC；③BE+CH=AE；④△AEC是等腰直角三角形.你认为正确的序号是（ ）

    A. ①②③ B. ①③④ C. ②③④ D. ①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD的顶点A（﹣2，3），B（﹣3，1），C（0，1），规定“平行四边形ABCD先沿x轴翻折，再向左平移1个单位”为一次变换，则连续经过2017次变换后，平行四边形ABCD的对角线的交点M的坐标为（ ）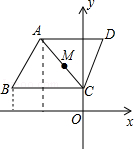
    A.（﹣2017，2）
    B.（﹣2017，﹣2）
    C.（﹣2018，﹣2）
    D.（﹣2018，2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，E是直线AB，CD内部一点，AB∥CD，连接EA，ED．

    （1）探究猜想：

    ①若∠A=20°，∠D=40°，则∠AED= °

    ②猜想图①中∠AED，∠EAB，∠EDC的关系，并用两种不同的方法证明你的结论．

    （2）拓展应用：

    如图②，射线FE与l1，l2交于分别交于点E、F，AB∥CD，a，b，c，d分别是被射线FE隔开的4个区域（不含边界，其中区域a，b位于直线AB上方，P是位于以上四个区域上的点，猜想：∠PEB，∠PFC，∠EPF的关系（任写出两种，可直接写答案）．

    查看答案和解析>>

    同步练习册答案