
分析 (1)根据零指数幂、绝对值、特殊角的三角函数值可以解答本题;
(2)根据分式的减法和除法可以化简题目中的式子,然后将a的值代入化简后的式子即可解答本题.
解答 解:(1)(π-2017)0+|2-$\sqrt{3}$|-4cos30°+$\root{3}{64}$
=1+$2-\sqrt{3}$-4×$\frac{\sqrt{3}}{2}$+4
=1+2-$\sqrt{3}-2\sqrt{3}$+4
=7-3$\sqrt{3}$;
(2)$\frac{{a}^{2}}{{a}^{2}+2a}$-$\frac{{a}^{2}-2a+1}{a+2}$÷$\frac{{a}^{2}-1}{a+1}$
=$\frac{{a}^{2}}{a(a+2)}-\frac{(a-1)^{2}}{a+2}•\frac{a+1}{(a+1)(a-1)}$
=$\frac{a}{a+2}-\frac{a-1}{a+2}$
=$\frac{1}{a+2}$,
当a=$\sqrt{2}-2$时,原式=$\frac{1}{\sqrt{2}-2+2}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$.
点评 本题考查分式的化简求值、零指数幂、绝对值、特殊角的三角函数值,解答本题的关键是明确它们各自的计算方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
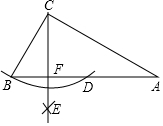 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,以点C为圆心,CB长为半径作弧,交AB于点D;再分别以点B和点D为圆心,大于$\frac{1}{2}$BD的长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则AF的长为( )
如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,以点C为圆心,CB长为半径作弧,交AB于点D;再分别以点B和点D为圆心,大于$\frac{1}{2}$BD的长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则AF的长为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则△ADE的周长为( )
如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则△ADE的周长为( )| A. | 8 | B. | 3 | C. | 9 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com