
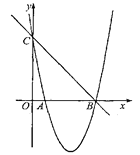
【题目】如图,已知抛物线y=x2+bx+c的图像与x轴的一个交点为A(1,0),另一个交点为B,且与y轴交于点C(0,5).
(1)求直线BC及抛物线的解析式;
(2)若点M是抛物线在x轴下方图像上的一动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图像上任意一点,以BC为边作□CBPQ,设□CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标.
【答案】(1)y=-x+5, y=x2-6x+5;(2)![]() ; (3)点P的坐标为P1(2,-3)(与点D重合)或P2(3,-4).
; (3)点P的坐标为P1(2,-3)(与点D重合)或P2(3,-4).
【解析】分析:(1)根据待定系数法,可得函数解析式,
(2)根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得二次函数,根据二次函数的性质,可由顶点式求解;
(3)先求出△ABN的面积和BC的长,再根据平行四边形的面积和△ABN的面积的关系,可得平行四边形高的长,根据等腰直角三角形,可得CE的长,根据待定系数法,可得PQ的解析式,根据解方程可得答案.
详解:(1)∵抛物线y=x2+bx+c与x轴的一个交点为A(1,0),与y轴交于点C(0,5),
∴将A(1,0),C(0,5)代入y=x2+bx+c,
解得:b=-6,c=5.
∴二次函数解析式为:y=x2-6x+5.
令y=0,求得另一交点B的坐标为(5,0)
设直线BC的解析式为:y=kx+5.
将B(5,0)代入直线BC解析式y=kx+5.
解得:k=-1.
∴直线BC的解析式为:y=-x+5.
(2)如图①.设M(x,y),则
NM=-x+5-(x2-6x+5).
NM=-x2+5x.
NM=-(x-![]() )2+
)2+![]() .
.
∴NM的最大值为![]() .
.
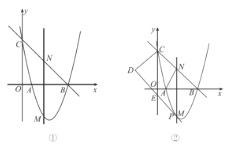
(3)如图②由第2问易得S2=5,∴S1=6S2=30.
BC=5![]() ,BC所在直线的解析式为:y=-x+5,
,BC所在直线的解析式为:y=-x+5,
∠CBO=45°,
∵S2=30.∴平行四边形CBPQ中BC边上的高为![]() .
.
过点C作CD⊥PQ与PQ所在直线相交于点D,
PD交y轴于点E,CD=3![]() ,∴CE=6,
,∴CE=6,
∵平行四边形CBPQ的边PQ所在直线,在直线BC的两侧可能各有一条,但点P在x轴下方,
∴PQ的解析式为y=-x-1.
∵点P同时在抛物线和直线PQ上,
∴x2-6x+5=-x-1.解得x1=2,x2=3,
∴P1(2,-3),P2(3,-4).


科目:初中数学 来源: 题型:
【题目】小虫从点A出发在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬行的路程依次为:(单位:cm)①+5,②-3,③+10,④-8,⑤-6,⑥+11,⑦-9.
(1)小虫最后是否回到出发点A,说明理由;
(2)小虫在第几次爬行后离点A最远,此时距离点A多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,那么小虫一共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )

A. 第3分时汽车的速度是40千米/时
B. 第12分时汽车的速度是0千米/时
C. 从第3分到第6分,汽车行驶了120千米
D. 从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,DE⊥BC交AC于点E,已知AD=AB,连接BE交AD于点F,下列结论:①BE=CE;②∠CAD=∠ABE;③S△ABF=3S△DEF;④△DEF∽△DAE,其中正确的有( )
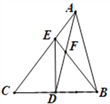
A. 1个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“水是生命之源”,某市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:
用水量/月 | 单价(元/m3) |
不超过20m3 | 2.8 |
超过20m3的部分 | 3.8 |
另:每立方米用水加收0.2元的城市污水处理费 | |
(1)根据上表,用水量每月不超过20m3,实际每立方米收水费_____元;如果1月份某用户用水量为19m3,那么该用户1月份应该缴纳水费____元;
(2)某用户2月份共缴纳水费80元,那么该用户2月份用水多少m3?
(3)若该用户水表3月份出了故障,只有70%的用水量记入水表中,这样该用户在3月份只缴纳了58.8元水费,问该用户3月份实际应该缴纳水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E. F,垂足为O.

(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.
(2)如图1,求AF的长.
(3)如图2,动点P、Q分别从A. C两点同时出发,沿△AFB和△CDE各边匀速运动一周。即点P自A→F→B→A停止,点Q自C→D→E→C停止。在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.
①问在运动的过程中,以A. P、C. Q四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t和点Q的速度;若不可能,请说明理由.
②若点Q的速度为每秒0.8cm,当A. P、C. Q四点为顶点的四边形是平行四边形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.
(1)2014年这种礼盒的进价是多少元/盒?
(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OC是∠AOB内部任意一条射线,OD,OE分别是∠AOC,∠BOC的角平分线,下列叙述正确的是( )

A. ∠AOD+∠BOE=60°B. ∠AOD=![]() ∠EOC
∠EOC
C. ∠BOE=2∠CODD. ∠DOE的度数不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,BD是正方形ABCD的对角线,BC=4,点H是AD边上的一动点,连接CH,作![]() ,使得HE=CH,连接AE。
,使得HE=CH,连接AE。
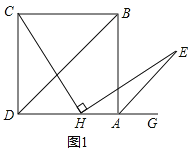

(1)求证:![]() ;
;
(2)如图2,过点E作EF//AD交对角线BD于点F,试探究:在点H的运动过程中,EF的长度是否为一个定值;如果是,请求出EF的长度。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com