
分析 直接利用平面向量的加减运算法则求解即可求得答案.
解答 解:2(2$\overrightarrow{a}$+3$\overrightarrow{b}$)-$\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$
=4$\overrightarrow{a}$+6$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$
=$\frac{11}{3}$$\overrightarrow{a}$+$\frac{13}{2}$$\overrightarrow{b}$.
故答案为:$\frac{11}{3}$$\overrightarrow{a}$+$\frac{13}{2}$$\overrightarrow{b}$.
点评 此题考查了平面向量的运算.注意掌握去括号时符号的变化是解此题的关键.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:解答题
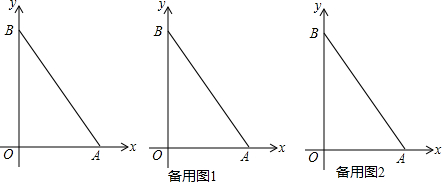
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲 | 8 | 6 | 7 | 8 | 9 | 10 | 6 | 5 | 4 | 7 |
| 乙 | 7 | 9 | 8 | 5 | 6 | 7 | 7 | 6 | 7 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
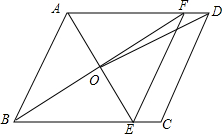 如图,在平行四边形ABCD中,AE平分∠BAD交BC于点E,BF平分∠ABC交AD于点F,AE、BF交于点O,连接EF、OD.
如图,在平行四边形ABCD中,AE平分∠BAD交BC于点E,BF平分∠ABC交AD于点F,AE、BF交于点O,连接EF、OD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
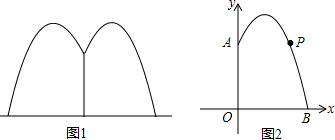
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
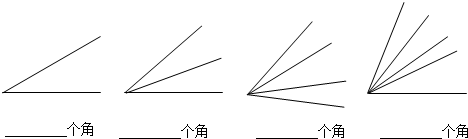
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
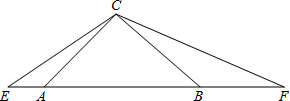 如图,在等腰三角形ABC中,∠ACB=90°,分别延长BA至点E,AB至点F,使得AE=2,且∠ECF=135°,若设AB=x,BF=y,试求出y与x之间的两数关系式.
如图,在等腰三角形ABC中,∠ACB=90°,分别延长BA至点E,AB至点F,使得AE=2,且∠ECF=135°,若设AB=x,BF=y,试求出y与x之间的两数关系式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com