
分析 根据勾股定理的逆定理得到∠ACB=90°,分三种情况①CM=BM,②BC=CM′=3,③BC=BM″=3,根据三角形的面积公式得到结果.
解答 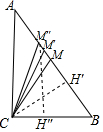 解:∵AB=5cm,BC=3cm,AC=4cm,
解:∵AB=5cm,BC=3cm,AC=4cm,
∴AC2+BC2=AB2,
∴∠ACB=90°,
①CM=BM,则M是AB的中点,
∴△BCM的面积=$\frac{1}{2}$S△ABC=3,
②BC=CM′=3,
过C作CH′⊥AB与H′,
∴CH′=$\frac{12}{5}$,BH′=$\frac{9}{5}$,
∴BM′=$\frac{18}{5}$,
∴△BCM的面积=$\frac{1}{2}×\frac{18}{5}$×$\frac{12}{5}$=$\frac{108}{25}$,
③BC=BM″=3,
∴△BCM的面积=$\frac{1}{2}×$3×$\frac{12}{5}$=$\frac{18}{5}$.
点评 本题考查了等腰三角形的性质,直角三角形的性质,三角形面积的计算,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | ${C_{13}}^5$ | B. | ${C_{13}}^6$ | C. | ${C_{13}}^{11}$ | D. | ${C_{12}}^7$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
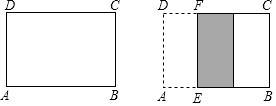 如图,在长方形纸片ABCD中,AB=15cm,AD=10cm.将纸片沿EF折叠,EF∥AD,设AE=x(cm),折叠后重叠部分的面积为S(cm2).
如图,在长方形纸片ABCD中,AB=15cm,AD=10cm.将纸片沿EF折叠,EF∥AD,设AE=x(cm),折叠后重叠部分的面积为S(cm2).| x/cm | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
| S/cm2 | 10 | 30 | 50 | 70 | 60 | 40 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
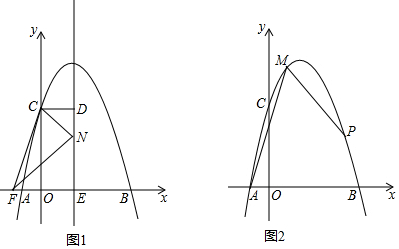
 如图,在平面直角坐标系中,O为坐标原点,抛物线F:y=ax2+2ax+c经过A(-4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.
如图,在平面直角坐标系中,O为坐标原点,抛物线F:y=ax2+2ax+c经过A(-4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
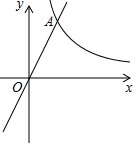 已知:如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0).
已知:如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com