
����Ŀ����1�����ⷢ��
��ͼ1����ACB����DCE��Ϊ�ȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
��գ��١�AEB�Ķ���Ϊ �����߶�AD��BE֮���������ϵΪ ��
��2����չ̽��
��ͼ2����ACB����DCE��Ϊ����ֱ�������Σ���ACB=��DCE=90������A��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����BE�����ж���AEB�Ķ������߶�CM��AE��BE֮���������ϵ����˵�����ɣ�

���𰸡�(1)��60������ȣ�(2)��2cm
��������
���������(1)�����ݵȱ������ε������Լ�������ȫ�ȵ����ʵó��𰸣�(2)��������ACD�ա�CEB�ó���CEB=��ADC=135��������AEB=135��-45��=90����Ȼ����ݵ���ֱ�������ε����ʵó���.
���������(1)��60�� ���
(2)���ߡ�ACD�ա�CEB ���CEB=��ADC=135�� ���AEB=135��-45��=90��
�ߡ�ACD�ա�CEB ��AD=BE �ڵ���ֱ��������CDE��CM=![]()
��AE-AD=DE ��AE-BE=2cm


 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������б���Ķ�Ӧֵ���ж�ax2+bx+c=0 ��a��0��a��b��cΪ��������һ����x��ȡֵ��Χ��_____
x | 3.23 | 3.24 | 3.25 | 3.26 |
ax2+bx+c | ��0.06 | ��0.02 | 0.03 | 0.09 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
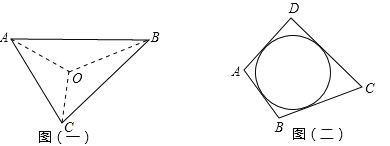
����Ŀ���Ķ����ϣ���ͼ(һ)����ABC���ܳ�Ϊ![]() ������ԲO�İ뾶Ϊr,����OA��OB��OC����ABC������Ϊ����С�����Σ���S��ABC��ʾ��ABC�����
������ԲO�İ뾶Ϊr,����OA��OB��OC����ABC������Ϊ����С�����Σ���S��ABC��ʾ��ABC�����
�� S��ABC=S��OAB+S��OBC+S��OCA
����S��OAB=![]() ��S��OBC=
��S��OBC=![]() ��S��OCA =
��S��OCA =![]()
��S��ABC=![]() +
+![]() +
+![]() =
=![]() (����Ϊ����������Բ�뾶��ʽ)
(����Ϊ����������Բ�뾶��ʽ)
(1)������Ӧ�ã����ù�ʽ���������Ϊ5��12��13������������Բ�뾶��
(2)��������������ı���ABCD��������Բ(�����߶����е�Բ����ͼ(��))������ΪS�����߳��ֱ�Ϊa��b��c��d�����Ƶ��ı��ε�����Բ�뾶��ʽ��
(3)��չ����������һ��n����(nΪ��С��3������)��������Բ��������ΪS�����߳�����Ϊa1��a2��a3������an����������������Բ�뾶��ʽ(����˵������)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�ķ���mx2��2mx+m+n��0������ʵ������
��1����ʵ��m��n�������������
��2��д��һ������������m��n��ֵ�������ʱ���̵ĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ�� A��һֻ���ϴ� A �������� 4 ����λ���ȵ���ԭ������� A ���� ʾ�����ǣ� ��
A. 4 B. ��4 C. ��8 D. ��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ�������
A. Ҫ�˽����о��꼶ѧ�������ߣ�Ӧ�����ղ�ķ�ʽ��
B. ���ӳɼ��ķ���Ϊ5���Ҷӳɼ��ķ���Ϊ3����ӳɼ������Ҷӳɼ��ȶ���
C. �����������ĸ�����99%����ô����һ�������ꣻ
D. һ������4��6��7��6��7��8��9����λ������������6��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com