
【题目】阅读材料:如图(一),△ABC的周长为![]() ,内切圆O的半径为r,连结OA、OB、OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积
,内切圆O的半径为r,连结OA、OB、OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积
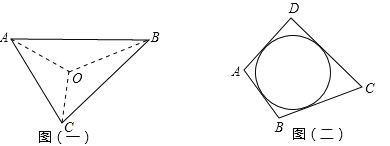
∵ S△ABC=S△OAB+S△OBC+S△OCA
又∵S△OAB=![]() ,S△OBC=
,S△OBC=![]() ,S△OCA =
,S△OCA =![]()
∴S△ABC=![]() +
+![]() +
+![]() =
=![]() (可作为三角形内切圆半径公式)
(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1、a2、a3、…、an,合理猜想其内切圆半径公式(不需说明理由).
【答案】(1)2;(2)r=![]() ;(3)r=
;(3)r=![]() .
.
【解析】
试题分析:(1)根据上述三角形的内切圆的半径公式,由已知条件,结合勾股定理的逆定理得该三角形是直角三角形.可以首先求得其面积是30,其周长是5+12+13=30.再根据其公式代入计算;
(2)同样连接圆心和四边形的各个顶点以及圆心和的切点,根据四边形的面积等于四个直角三角形的面积进行计算;
(3)根据上述方法和结论,即可猜想到:任意多边形的内切圆的半径等于其面积的2倍除以多边形的周长.
试题解析:(1)以5,12,13为边长的三角形为直角三角形,易求得r=![]()
(2)连接OA,OB,OC,OD,并设内接圆半径为r,
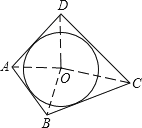
可得S四边形ABCD=S△OAB+S△OBC+S△OCD+S△ODA
=![]() a
a![]() r+
r+![]() b
b![]() r+
r+![]() c
c![]() r+
r+![]() d
d![]() r=
r=![]() (a+b+c+d)
(a+b+c+d)![]() r.
r.
∴r=![]() ;
;
(3)猜想:r=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:如果(x+1)2﹣9=0,那么(x+1)2﹣32=(x+1+3)(x+1﹣3)=(x+4)(x﹣2),则(x+4)(x﹣2)=0,由此可知:x1=﹣4,x2=2.根据以上材料计算x2﹣6x﹣16=0的根为( )
A.x1=﹣2,x2=8B.x1=2,x2=8
C.x1=﹣2,x2=﹣8D.x1=2,x2=﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中,小格的顶点叫做格点。小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连结三个格点,使之构成直角三角形。小华在左边的正方形网格中作出了Rt⊿ABC。请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:①∠AEB的度数为 ;②线段AD,BE之间的数量关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c是三角形的三边长,如果满足(a﹣5)2+|b﹣12|+c2﹣26c+169=0,则三角形的形状是( )
A.底与边不相等的等腰三角形
B.等边三角形
C.钝角三角形
D.直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
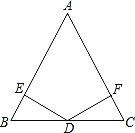
(1)求证:△BED≌△CFD;
(2)若∠A=60°,BE=2,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com