
 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
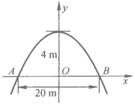
.有一座抛物线型拱桥(如图所示),正常水位时桥下河面宽20 m,河面距拱顶4 m. 试求:
(1)在如图26-10所示的平面直角坐标系中,求出抛物线解析式;
(2)为了保证过往船只顺利航行,桥下水面的宽度不得小于18m,求水面在正常水位基础上涨多少米时,就会影响过往船只?
查看答案和解析>>
科目:初中数学 来源: 题型:
 抛物线的对称轴是直线x=1.5,且图象过点A(0, ﹣4)和点B(4,0),
抛物线的对称轴是直线x=1.5,且图象过点A(0, ﹣4)和点B(4,0),
(1)求抛物线的解析式;
(2)若抛物线与x轴的另一个交点为C,M是线段BC上的任意一点,当△MAB为等腰三角形时,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
绿豆在相同条件下的发芽试验,结果如下表所示:
| 每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
| 发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1912 | 2850 |
| 发芽的频数 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.956 | 0.950 |
则绿豆发芽的概率估计值是 ( )
A.0.96 B.0.95 C.0.94 D.0.90
查看答案和解析>>
科目:初中数学 来源: 题型:
在利用图象法求方程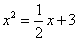 的解
的解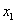 ,
,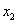 时,下面是四位同学的解法:
时,下面是四位同学的解法:
(1)函数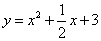 的图象与x轴交点的横坐标为
的图象与x轴交点的横坐标为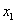 、
、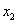 ;
;
(2)函数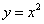 和
和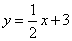 的图象交点的横坐标为
的图象交点的横坐标为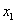 、
、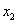 ;
;
(3)函数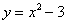 和
和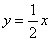 的图象交点的横坐标为
的图象交点的横坐标为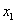 、
、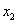 ;
;
(4)函数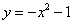 和
和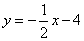 的图象交点的横坐标为
的图象交点的横坐标为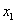 、
、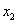 ;
;
你认为正确解法的同学有 (填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,菱形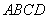 的边长为6厘米,
的边长为6厘米, .从初始时刻开始,点
.从初始时刻开始,点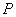 、
、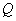 同时从
同时从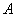 点出发,点
点出发,点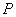 以1厘米/秒的速度沿
以1厘米/秒的速度沿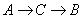 的方向运动,点
的方向运动,点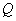 以2厘米/秒的速度沿
以2厘米/秒的速度沿 的方向运动,当点
的方向运动,当点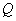 运动到
运动到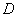 点时,
点时,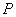 、
、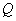 两点同时停止运动,设
两点同时停止运动,设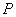 、
、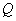 运动的时间为
运动的时间为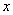 秒时,
秒时,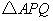 与
与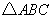 重叠部分的面积为
重叠部分的面积为 平方厘米(这里规定:点和线段是面积为0的三角形),解答下列问题:
平方厘米(这里规定:点和线段是面积为0的三角形),解答下列问题:
(1)点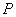 、
、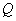 从出发到相遇所用时间是 秒;
从出发到相遇所用时间是 秒;
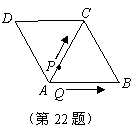 (2)点
(2)点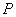 、
、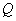 从开始运动到停止的过程中,当
从开始运动到停止的过程中,当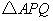 是等边三角形时
是等边三角形时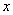
 的值是 秒;
的值是 秒;
( 3)当0≤
3)当0≤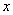 ≤6时,求
≤6时,求 与
与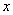 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
△ABC中,BC=18,AC=12,AB=9,点D,E分别是直线AB,AC上的两个点,AE=4.
若由A,D,E构成的三角形与△ABC相似,则DB的长为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com