
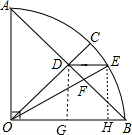
 如图,已知
如图,已知 |
| AB |
 |
| AB |
 |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 如图,要测量水池对岸A、B的距离,如果测得AC、BC、DC的长分别为48m、72m、12m,那么只要在BC取点E,使CE=
如图,要测量水池对岸A、B的距离,如果测得AC、BC、DC的长分别为48m、72m、12m,那么只要在BC取点E,使CE=查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
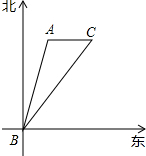 小明在课外实践活动中,在B处观测某建筑物A在北偏东15°方向,小明沿东北方向的公路BC以10km/h的速度前进,30min到达C处,测得A在正西方向,求建筑物A到BC的距离.
小明在课外实践活动中,在B处观测某建筑物A在北偏东15°方向,小明沿东北方向的公路BC以10km/h的速度前进,30min到达C处,测得A在正西方向,求建筑物A到BC的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com