
【题目】已知,BC∥OA,∠B=∠A=100°,试回答下列问题: 
(1)如图①,求证:OB∥AC.
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于;(在横线上填上答案即可).
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
(4)在(3)的条件下,如果平行移动AC的过程中,若使∠OEB=∠OCA,此时∠OCA度数等于 . (在横线上填上答案即可).
【答案】
(1)证明:∵BC∥OA,
∴∠B+∠O=180°,
∴∠O=180°﹣∠B=80°,
而∠A=100°,
∴∠A+∠O=180°,
∴OB∥AC
(2)40°
(3)解:不改变.
∵BC∥OA,
∴∠OCB=∠AOC,∠OFB=∠AOF,
∵∠FOC=∠AOC,
∴∠AOF=2∠AOC,
∴∠OFB=2∠OCB,
即∠OCB:∠OFB的值为1:2
(4)60°
【解析】(2)解:∵OE平分∠BOF,
∴∠BOE=∠FOE,
而∠FOC=∠AOC,
∴∠EOF+∠COF= ![]() ∠AOB=
∠AOB= ![]() ×80°=40°;(4)解:设∠AOC的度数为x,则∠OFB=2x,
×80°=40°;(4)解:设∠AOC的度数为x,则∠OFB=2x,
∵∠OEB=∠AOE,
∴∠OEB=∠EOC+∠AOC=40°+x,
而∠OCA=180°﹣∠AOC﹣∠A=180°﹣x﹣100°=80°﹣x,
∵∠OEB=∠OCA,
∴40°+x=80°﹣x,解得x=20°,
∴∠OCA=80°﹣x=80°﹣20°=60°.
所以答案是40°,60°.
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


科目:初中数学 来源: 题型:
【题目】已知a,b是实数,x=a2+b2+24,y=2(3a+4b),则x,y的大小关系是( )
A. x≤y B. x≥y C. x<y D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2. 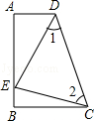
(1)求证:Rt△ADE与Rt△BEC全等;
(2)求证:△CDE是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于A、B(A点在B点的左侧)与
轴交于A、B(A点在B点的左侧)与![]() 轴交于点C.
轴交于点C.
(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;
(2)如图2,点P为第四象限抛物线上一点,连接PC,若![]() 时,求点P的横坐标;
时,求点P的横坐标;
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥![]() 轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=
轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=![]() ,连接KB并延长交抛物线于点Q,求PQ的长.
,连接KB并延长交抛物线于点Q,求PQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形. 
(1)(i)已知点A在格点(即小正方形的顶点)上,画一条线段AB,长度为 ![]() ,且点B在格点上. (ii)以上题所画的线段AB为一边,另外两条边长分别为
,且点B在格点上. (ii)以上题所画的线段AB为一边,另外两条边长分别为 ![]() ,
, ![]() .画一个△ABC,使点C在格点上(只需画出符合条件的一个三角形).
.画一个△ABC,使点C在格点上(只需画出符合条件的一个三角形).
(2)所画出的△ABC的边AB上的高线长为 . (直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划从办公用品公司购买A,B两种型号的小黑板.经洽谈,购买一块A型小黑板比购买一块B型小黑板多用20元,且购买5块A型小黑板和4块B型小黑板共需820元.
(1)求购买一块A型小黑板、一块B型小黑板各需多少元.
(2)根据该中学实际情况,需从公司购买A,B两种型号的小黑板共60块,要求购买A,B两种型号小黑板的总费用不超过5240元.并且购买A型小黑板的数量不小于购买B型小黑板数量的 ![]() .则该中学从公司购买A,B两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
.则该中学从公司购买A,B两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com