
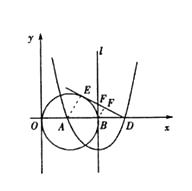
【题目】如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求DE的长;
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长 .
【答案】
(1)解:由题意可知,抛物线的对称轴为:x=6
∴设抛物线的解析式为 ![]()
∵抛物线经过点A(3,0)和C(0,9)
∴ ![]()
解得: ![]() ,k=-3
,k=-3
∴ ![]()
(2)解:连接AE
∵DE是⊙A的切线,∴∠AED=90°,AE=3
∵直线l是抛物线的对称轴,点A,D是抛物线与x轴的交点
∴AB=BD=3
∴AD=6
在Rt△ADE中, ![]()
∴ ![]()
(3)解:)当BF⊥ED时∵∠AED=∠BFD=90°∠ADE=∠BDF
∴△AED∽△BFD
∴ ![]() 即
即 ![]()
∴ ![]()
当FB⊥AD时∵∠AED=∠FBD=90°∠ADE=∠FDB
∴△AED∽△FBD ∴ ![]() 即
即 ![]()
∴当△BFD与EAD△相似时,BF的长为 ![]() 或
或 ![]()
【解析】(1)根据题意可知此抛物线的对称轴为x=6,设抛物线的解析式为顶点式,再将点A、C两点坐标代入解析式,建立方程求解,即可求出此函数解析式。
(2) 由DE是⊙A的切线,因此添加辅助线连接AE,得出∠AED=90°,AE=3 ,再根据圆的对称性及抛物线的对称性,求出AD的长, 在Rt△ADE中,利用勾股定理求出DE的长。
(3)抓住已知点F是切线DE上的一个动点,要使△BFD与△EAD相似,图形中隐含公共角∠ADE=∠BDF,因此分两种情况:当BF⊥ED时;当FB⊥AD时,根据相似三角形的性质,得出对应边成比例,建立方程,即可求出BF的长。
【考点精析】掌握二次函数的性质和勾股定理的概念是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)计算并观察下列各式:
第1个:(a﹣b)(a+b)=______;
第2个:(a﹣b)(a2+ab+b2)=______;
第3个:(a﹣b)(a3+a2b+ab2+b3)=_______;
……
这些等式反映出多项式乘法的某种运算规律.
(2)猜想:若n为大于1的正整数,则(a﹣b)(an﹣1+an﹣2b+an﹣3b2+……+a2bn﹣3+abn﹣2+bn﹣1)=________;
(3)利用(2)的猜想计算:2n﹣1+2n﹣2+2n﹣3+……+23+22+1=______.
(4)拓广与应用:3n﹣1+3n﹣2+3n﹣3+……+33+32+1=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A对应的数为a,点B对应的数为b,且多项式﹣![]() x2y﹣
x2y﹣![]() xy2﹣2xy+5的次数为a,常数项为b.
xy2﹣2xy+5的次数为a,常数项为b.
(1)直接写出a、b的值;
(2)数轴上点A、B之间有一动点P(不与A、B重合),若点P对应的数为x,试化简:|2x+6|+4|x﹣5|﹣|6﹣x|+|3x﹣9|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了预测本校应届毕业女生“一分钟跳绳”项目考试情况,从九年级随机抽取部分女生进行该项目测试,并以测试数据为样本,绘制出如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图.根据统计图提供的信息解答下列问题: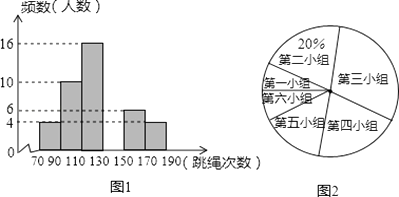
(1)补全频数分布直方图 , 并指出这个样本数据的中位数落在第小组;(1)
(2)若测试九年级女生“一分钟跳绳”次数不低于130次的成绩为优秀,本校九年级女生共有260人,请估计该校九年级女生“一分钟跳绳”成绩为优秀的人数;
(3)如测试九年级女生“一分钟跳绳”次数不低于170次的成绩为满分,在这个样本中,从成绩为优秀的女生中任选一人,她的成绩为满分的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F.
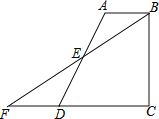
(1)请连结AF、BD,试判断四边形ABDF是何种特殊四边形,并说明理由.
(2)若AB=4,BC=5,CD=6,求△BCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(给出定义)
数轴上顺次有三点A、C、B,若点C到点A的距离是点C到点B的距离的3倍,我们就称点C是(A、B)的“梦想点”例如:图①中,点A、B表示的数分别为-2、2,表示数1的点C是(A、B)的“梦想点”;图②中,点A、B表示对的数分别为-2、2,表示-1的点C是(B、A)的“梦想点.

(解决问题)
(1)若数轴上M、N两点所表示的数分别为![]() 且
且![]() 满足
满足![]() 求出(M、N)的“梦想点”表示的数;
求出(M、N)的“梦想点”表示的数;
(2)如图③,在数轴上点A、B表示的数分别为-15和65,点P从点A出发沿数轴向右运动:
①若点P运动到点B停止,则当P、A、B中恰好有一个点为其余两个点的“梦想点”时,求这个点表示的数;
②若点P运动到B后,继续沿数轴向右运动的过程中,是否还存在点P、A、B中恰好有一个点为其余两点的“梦想点”的情况?若存在,请直接写出此时以PA、PB为邻边长的长方形的周长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。
(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com