
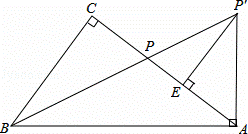
如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P′),当AP旋转至AP′⊥AB时,点B、P、P′恰好在同一直线上,此时作P′E⊥AC于点E.
(1)求证:∠CBP=∠ABP;
(2)求证:AE=CP;
(3)当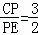 ,BP′=5
,BP′=5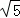 时,求线段AB的长.
时,求线段AB的长.
(1)证明:∵AP′是AP旋转得到,
∴AP=AP′,
∴∠APP′=∠AP′P,
∵∠C=90° ,AP′⊥AB,
,AP′⊥AB,
∴∠CBP+∠BPC=90°,∠ABP+∠AP′P=90°,
又∵∠BPC=∠APP′(对顶角相等),
∴∠CBP=∠ABP;
(2)证明:如图,过点P作PD⊥AB于D,
∵∠CBP=∠ABP,∠C=90°,
∴CP=DP,
∵P′E⊥AC,
∴∠EAP′+∠AP′E=90°,
又∵∠PAD+∠EAP′=90°,
∴∠PAD=∠AP′E,
在△APD和△P′AE中,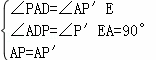 ,
,
∴△APD≌△P′AE(AAS),
∴AE=DP,
∴AE=CP;
(3)解:∵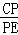 =
=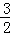 ,
,
∴设CP =3k,PE=2k,
=3k,PE=2k,
则AE=CP=3k,AP′=AP=3k+2k=5k,
在Rt△AEP′中,P′E=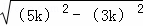 =4k,
=4k,
∵∠C=90°,P′E⊥AC,
∴∠CBP+∠BPC=90°,∠EP′P+∠P′PE=90°,
∵∠BPC=∠EPP′(对顶角相等),
∴∠CBP=∠P′PE,
又∵∠BAP′=∠P′EP=90°,
∴△ABP′∽△EPP′,
∴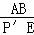 =
=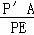 ,
,
即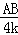 =
= ,
,
解得P′A=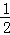 AB,
AB,
在Rt△ABP′中,AB2+P′A2=BP′2,
即AB2+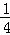 AB2=(5
AB2=(5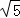 )2,
)2,
解得AB=10.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
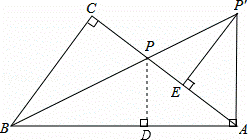
将量角器按如图所示的方式放置在三角形纸片上,使点C在半圆圆心上,点B在半圆上,边AB、AC分别交半圆于点E、F,点B、E、F对应的读数分别为160°、70°、50°,则∠A的度数为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
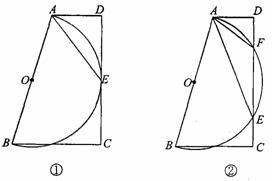
在梯形ABCD中,AD∥BC,∠D=90°,以AB为直径作⊙O.
(1)如图①,⊙O与DC相切于点E,试说明:∠BAE=∠DAE;
(2)如图②,⊙O与DC交于点E、F.
①图中哪一个角与∠BAE相等?为什么?
②试探究线段DF与CE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )

查看答案和解析>>
科目:初中数学 来源: 题型:
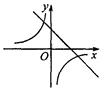
一次函数y=kx+b与反比例函数y=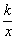 的图像如图所示,下列结论正确的是 ( )
的图像如图所示,下列结论正确的是 ( )
A.它们的函数值y随着x的增大而增大
B.它们的函数值y随着x的增大而减小
C.k<0
D.它们的自变量x的取值为全体实数
查看答案和解析>>
科目:初中数学 来源: 题型:
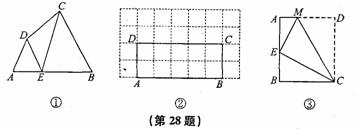
如图①,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把点E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把点E叫做四边形ABCD的边AB上的强相似点,解决问题:
(1)如图①,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图②,在矩形ABCD中,AB=5,BC=2,且A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
2014年3月14日,“玉兔号”月球车成功在距地球约384 400公里远的月球上自主唤醒,将384 400精确到万位用科学记数法表示为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com