
 阅读理解:对于任意正实数a,b,$Q(\sqrt{a}-\sqrt{b})^{2}≥0$,
阅读理解:对于任意正实数a,b,$Q(\sqrt{a}-\sqrt{b})^{2}≥0$,分析 (1)根据已知条件,当2x=$\frac{6}{x}$时,$2x+\frac{6}{x}$ 有最小值,进而求出即可;
(2)首先利用S四边形ABCD=S△ACD +S△ABC,再结合当$\frac{6}{x}$=$\frac{3}{2}$x时SABCD的面积最小,求出x的值,进而得出答案;
(3)首先设y′=$\frac{{x}^{2}-2x+25}{x}$=x-2+$\frac{25}{x}$,当x=$\frac{25}{x}$时y'最小,进而得出x的值以及y的值.
解答 解:(1)当2x=$\frac{6}{x}$时,则x2=3,
解得x=±$\sqrt{3}$,
∵x>0,
∴x=$\sqrt{3}$,
∴$2x+\frac{6}{x}$ 有最小值是4$\sqrt{3}$.
故答案为:$\sqrt{3}$,4$\sqrt{3}$;
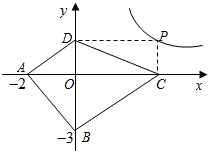
(2)设点P的坐标为(x,$\frac{6}{x}$),
∵PC⊥x轴于点C,PD⊥y轴于点D,
∴OC=x,OD=$\frac{6}{x}$,
∴S△ACD=$\frac{1}{2}$×AC×OD=$\frac{1}{2}$(x+2)×$\frac{6}{x}$=$\frac{3(x+2)}{x}$,
S△ABC=$\frac{1}{2}$×AC×OB=$\frac{1}{2}$(x+2)×3=$\frac{3}{2}$(x+2),
S四边形ABCD=S△ACD +S△ABC=$\frac{3(x+2)}{x}$+$\frac{3}{2}$(x+2)=$\frac{6}{x}$+$\frac{3x}{2}$+6,
当$\frac{6}{x}$=$\frac{3}{2}$x时SABCD的面积最小,解得x1=2,x2=-2(舍去),
∴当x=2时,S四边形ABCD=3+3+6=12,
∴四边形ABCD面积的最小值为12,
∵OD=$\frac{6}{2}$=3=OB,OC=2=OA,
∴四边形ABCD是平行四边形;
(3)设y′=$\frac{{x}^{2}-2x+25}{x}$=x-2+$\frac{25}{x}$,
当x=$\frac{25}{x}$时y'最小,
∴当x=5时,y'最小=8,
∴当x=5时,y最大=$\frac{1}{8}$.
点评 此题主要考查了反比例函数综合以及四边形面积公式和函数最值求法等知识,利用已知得出当$\frac{3x}{2}$=$\frac{6}{x}$时SABCD的面积最小进而得出x的值是解题关键.


科目:初中数学 来源: 题型:解答题
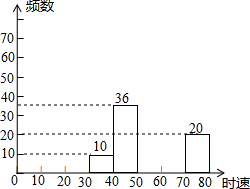 为保证全运会期间交通顺畅,在连接全运村、场馆及客运枢纽的干道上,将设置全运专用车道.同时交通部门对周边街路进行雷达测速区检测,现将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数及频率图表.
为保证全运会期间交通顺畅,在连接全运村、场馆及客运枢纽的干道上,将设置全运专用车道.同时交通部门对周边街路进行雷达测速区检测,现将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数及频率图表.| 数据段 | 频数 | 频率 |
| 30~40 | 10 | 0.05 |
| 40~50 | 36 | 0.18 |
| 50~60 | 78 | 0.39 |
| 60~70 | 56 | 0.28 |
| 70~80 | 20 | 0.10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 根据下表所列数据,制作扇形统计图表示小明一天的时间安排:
根据下表所列数据,制作扇形统计图表示小明一天的时间安排:| 项目 | 时间/h | 所占的百分比 | 对应的扇形圆心角的度数 |
| 睡觉 | 9 | ||
| 活动 | 4 | ||
| 学习 | 8 | ||
| 吃饭 | 1 | ||
| 其他 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com