
分析 列表或树状图将所有等可能的结果列举出来,然后利用概率公式求解即可.
解答 解:列表如下:
| -3 | -1 | 0 | 1 | 3 | |
| -3 | --- | (-1,-3) | (0,-3) | (1,-3) | (3,-3) |
| -1 | (-3,-1) | --- | (0,-1) | (1,-1) | (3,-1) |
| 0 | (-3,0) | (-1,0) | --- | (1,0) | (3,0) |
| 1 | (-3,1) | (-1,1) | (0,1) | --- | (3,1) |
| 3 | (-3,3) | (-1,3) | (0,3) | (1,3) | --- |
点评 本题考查了列表法与树状图的知识,解题的关键是能够将所有等可能的结果列举出来.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{7}{10}$ | C. | $\frac{7}{11}$ | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
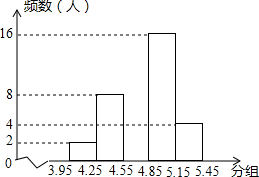 青少年视力水平下降已引起全社会的广泛关注,为了了解某市5000名初中毕业生的视力情况.我们从中抽取了一部分学生的视力作为样本进行数据处理,得到如下的频数分布表和频数分布直方图:
青少年视力水平下降已引起全社会的广泛关注,为了了解某市5000名初中毕业生的视力情况.我们从中抽取了一部分学生的视力作为样本进行数据处理,得到如下的频数分布表和频数分布直方图:| 分组 | 频数 | 频率 |
| 3.95~4.25 | 2 | 0.04 |
| 4.25~4.55 | 8 | 0.16 |
| 4.55~4.85 | 20 | 0.40 |
| 4.85~5.15 | 16 | 0.32 |
| 5.15~5.45 | 4 | 0.08 |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读理解:对于任意正实数a,b,$Q(\sqrt{a}-\sqrt{b})^{2}≥0$,
阅读理解:对于任意正实数a,b,$Q(\sqrt{a}-\sqrt{b})^{2}≥0$,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com