练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．先化简，再求值：$\frac{{x}^{2}}{x-1}$+$\frac{1}{1-x}$，其中x=$\sqrt{3}$-1．

    分析 先根据分式混合运算的法则把原式进行化简，再把x的值代入进行计算即可．

    解答 解：原式=$\frac{{x}^{2}}{x-1}$-$\frac{1}{x-1}$
    =$\frac{（x+1）（x-1）}{x-1}$
    =x+1，
    当x=$\sqrt{3}$-1时，原式=$\sqrt{3}$．

    点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

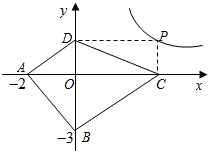    18．阅读理解：对于任意正实数a，b，$Q（\sqrt{a}-\sqrt{b}）^{2}≥0$，
    ∴$a-2\sqrt{ab}+b≥0$，
    ∴a+b≥2$\sqrt{ab}$，当且仅当a=b时，等号成立．
    结论：在a+b≥2$\sqrt{ab}$（a，b均为正实数）中，若ab为定值p，则$a+b≥2\sqrt{p}$，
    当且仅当a=b，a+b有最小值2$\sqrt{p}$．
    根据上述内容，回答下列问题：
    （1）若x＞0，只有当x=$\sqrt{3}$时，$2x+\frac{6}{x}$ 有最小值4$\sqrt{3}$．
    （2）探索应用：如图，已知A（-2，0），B（0，-3），点P为双曲线y=$\frac{6}{x}$（x＞0）上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D．求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．
    （3）已知x＞0，则自变量x为何值时，函数y=$\frac{x}{{x}^{2}-2x+25}$取到最大值，最大值为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．如图，直线a∥b，直线c分别与a，b相交，∠1=40°，则∠2的度数为（　　）
    A．150°B．140°C．100°D．40°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．计算：
    （1）2（x+y）2-（2x+y）（x-2y）
    （2）$（a-1+\frac{2-2a}{a+1}）÷\frac{{{a^2}-2a+1}}{{{a^2}-1}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．如图，AB∥CD，CM平分∠BCD，CN⊥CM，∠B=48°，则∠DCM=24°，∠BCN=66°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

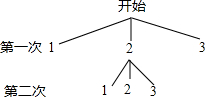    13．在一个不透明的口袋中有三张卡片，卡片上分别标有数字1，2，3，每张卡片除数字不同外其它都相同，小明同学先从袋子中随机抽出一张卡片，记下数字后放回并搅匀；再从袋子中随机抽出一张卡片记下数字．小明同学用画树状图的方法寻求他两次抽取卡片的所有可能结果．如图是小明同学所画的正确树状图的一部分．
    （1）补全小明同学所画的树状图；
    （2）求小明同学两次抽到卡片上的数字之积是奇数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．我们把不相等的两个实数a，b中较大实数a记作max{a，b}=a，例如：max{2.3，3.4}=3.4，
    max{-5.6，-8.7}=-5.6，max{-3，0}=0…那么：关于x的方程$max\left\{{x，-x}\right\}=\frac{2x+1}{x}$的解是-1或$1+\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．一个不透明的盒子中装有2枚黑色的棋子和1枚白色的棋子，每枚棋子除了颜色外其余均相同．从盒中随机摸出一枚棋子，记下颜色后放回并搅匀，再从盒子中随机摸出一枚棋子，记下颜色，用画树状图（或列表）的方法，求两次摸出的棋子颜色不同的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．完成下列各题
    （1）如图1△ABC中∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于E．求证：△ACD≌△AED．
    （2）如图2，∠1与∠D互余，CF⊥DF．求证：AB∥CD．

    查看答案和解析>>

    同步练习册答案