Question

【题目】在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且AE=BD，
（1）当点E为AB的中点时，如图1，求证：EC=ED；

（2）当点E不是AB的中点时，如图2，过点E作EF∥BC，求证：△AEF是等边三角形；

（3）在第（2）小题的条件下，EC与ED还相等吗，请说明理由．

Answer 1

【答案】
（1）证明：如图1，在等边△ABC中，AB=BC=AC，

∴∠ABC=∠ACB=∠A=60°，

∵AE=EB=BD，

∴∠ECB= ∠ACB=30°，∠EDB=∠DEB= ∠ACB=30°，

∴∠EDB=∠ECB，

∴EC=ED

（2）证明：如图2，∵EF∥BC，

∴∠AEF=∠ABC=60°，∠AFE=∠C=60°，

∴△AEF为等边三角形

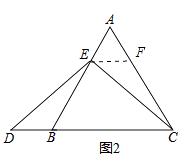
（3）证明：EC=ED；

理由：∵∠AEF=∠ABC=60°，

∴∠EFC=∠DBE=120°，

∵AB=AC，AE=AF，

∴AB﹣AE=AC﹣AF，即BE=FC，

在△DBE和△EFC中，

，

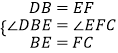∴△DBE≌△EFC（SAS），

∴ED=EC．

【解析】（1）根据等边三角形三线合一的性质可得∠ECB=30°，∠ABC=60°，根据AE=EB=BD，可得∠ECB= ∠ACB=30°，∠EDB=∠DEB= ∠ACB=30°，根据等角对等边即可证得结论；（2）根据平行线的性质证得∠AEF=∠ABC=60°，∠AFE=∠C=60°，即可证得结论；（3）先求得BE=FC，然后证得△DBE≌△EFC即可；