
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
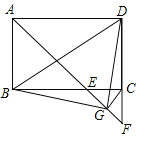
①BE=CD;
②∠DGF=135°;
③∠ABG+∠ADG=180°;
④若![]() ,则
,则![]() .
.
其中正确的结论是 .(填写所有正确结论的序号)
【答案】①③④.
【解析】
先求出∠BAE=45°,判断出△ABE是等腰直角三角形,根据等腰直角三角形的性质可得AB=BE,∠AEB=45°,从而得到BE=CD,故①正确;
再求出△CEF是等腰直角三角形,根据等腰直角三角形的性质可得CG=EG,再求出∠BEG=∠DCG=135°,然后利用“边角边”证明△DCG≌△BEG,得到∠BGE=∠DGC,由∠BGE<∠AEB,得到∠DGC=∠BGE<45°,∠DGF<135°,故②错误;
由于∠BGE=∠DGC,得到∠ABG+∠ADG=∠ABC+∠CBG+∠ADC-∠CDG=∠ABC+∠ADC=180°,故③正确;
由△BGD是等腰直角三角形得到BD=![]() =
=![]() ,求得S△BDG,过G作GM⊥CF于M,求得S△DGF,进而得出答案.
,求得S△BDG,过G作GM⊥CF于M,求得S△DGF,进而得出答案.
∵AE平分∠BAD,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,∠AEB=45°,
∵AB=CD,
∴BE=CD,故①正确;
∵∠CEF=∠AEB=45°,∠ECF=90°,
∴△CEF是等腰直角三角形,
∵点G为EF的中点,
∴CG=EG,∠FCG=45°,
∴∠BEG=∠DCG=135°,
在△DCG和△BEG中,
∵BE=CD,∠BEG=∠DCG,CG=EG,
∴△DCG≌△BEG(SAS).
∴∠BGE=∠DGC,
∵∠BGE<∠AEB,
∴∠DGC=∠BGE<45°,
∵∠CGF=90°,
∴∠DGF<135°,故②错误;
∵∠BGE=∠DGC,
∴∠ABG+∠ADG=∠ABC+∠CBG+∠ADC﹣∠CDG=∠ABC+∠ADC=180°,故③正确;
∵△DCG≌△BEG,
∵∠BGE=∠DGC,BG=DG,
∵∠EGC=90°,
∴∠BGD=90°,
∵BD=![]() =
=![]() ,
,
∴BG=DG=![]() ,
,
∴S△BDG=![]() =
=![]() ,
,
∴3S△BDG=![]() ,过G作GM⊥CF于M,
,过G作GM⊥CF于M,
∵CE=CF=BC﹣BE=BC﹣AB=1,
∴GM=![]() CF=
CF=![]() ,
,
∴S△DGF=![]() DFGM=
DFGM=![]() =
=![]() ,
,
∴13S△DGF=![]() ,
,
∴![]() ,故④正确.
,故④正确.
故答案为:①③④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() 的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+
的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+![]() =0的根的情况是________________.
=0的根的情况是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节能又环保的油电混合动力汽车,既可以用油做动力行驶,也可以用电做动力行驶,某品牌油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,则费用为80元;若完全用电做动力行驶,则费用为30元,已知汽车行驶中每千米用油费用比用电费用多0.5元.
(1)求:汽车行驶中每千米用电费用是多少元?甲、乙两地的距离是多少千米?
(2)若汽车从甲地到乙地采用油电混合动力行驶,且所需费用不超过50元,则至少需要用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB经过x轴上的点A(2,0),且与抛物线相交于B、C两点,已知B点坐标为(1,1) .
(1)求直线和抛物线的解析式;
(2)如果D为抛物线上一点,使得△AOD与△OBC的面积相等,求D点坐标。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某精品店购进甲、乙两种小礼品,已知1件甲礼品的进价比1件乙礼品的进价多1元,购进2件甲礼品与1件乙礼品共需11元.
(1)求甲礼品的进价;
(2)经市场调查发现,若甲礼品按6元/件销售,则每天可卖40件;若按5元/件销售,则每天可卖60件.假设每天销售的件数y(件)与售价x(元/件)之间满足一次函数关系,求y与x之间的函数解析式;
(3)在(2)的条件下,当甲礼品的售价定为多少时,才能使每天销售甲礼品的利润为60元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在利用描点法画二次函数y=ax2+bx+c(a=0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣3 | 0 | ﹣1 | 0 | ﹣3 | … |
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线C1:y=ax2﹣2ax+c(a<0)与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线C1的顶点为G.
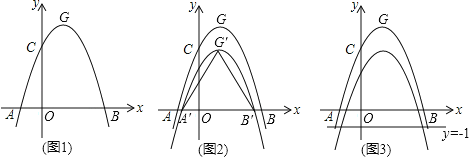
(1)求出抛物线C1的解析式,并写出点G的坐标;
(2)如图2,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2,设C2与x轴的交点为A′、B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值:
(3)在(2)的条件下,如图3,设点M为x轴正半轴上一动点,过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点,试探究在直线y=﹣1上是否存在点N,使得以P、Q、N为顶点的三角形与△AOQ全等,若存在,直接写出点M,N的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点,与y轴交于C点,B点与C点是直线y=x﹣3与x轴、y轴的交点.D为线段AB上一点.
与x轴交于A、B两点,与y轴交于C点,B点与C点是直线y=x﹣3与x轴、y轴的交点.D为线段AB上一点.

(1)求抛物线的解析式及A点坐标.
(2)若点D在线段OB上,过D点作x轴的垂线与抛物线交于点E,求出点E到直线BC的距离的最大值.
(3)D为线段AB上一点,连接CD,作点B关于CD的对称点B′,连接AB′、B′D
①当点B′落坐标轴上时,求点D的坐标.
②在点D的运动过程中,△AB′D的内角能否等于45°,若能,求此时点B′的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com