
����Ŀ��ij��Ʒ�깺���ס�������С��Ʒ����֪1������Ʒ�Ľ��۱�1������Ʒ�Ľ��۶�1Ԫ������2������Ʒ��1������Ʒ����11Ԫ��
��1�������Ʒ�Ľ��ۣ�
��2�����г����鷢�֣�������Ʒ��6Ԫ/�����ۣ���ÿ�����40��������5Ԫ/�����ۣ���ÿ�����60��������ÿ�����۵ļ���y���������ۼ�x��Ԫ/����֮������һ�κ�����ϵ����y��x֮��ĺ�������ʽ��
��3���ڣ�2���������£�������Ʒ���ۼ۶�Ϊ����ʱ������ʹÿ�����ۼ���Ʒ������Ϊ60Ԫ��
���𰸡���1������Ʒ�Ľ���Ϊ4Ԫ/������2��y����20x+160����3��������Ʒ���ۼ۶�Ϊ5Ԫ��7Ԫʱ������ʹÿ�����ۼ���Ʒ������Ϊ60Ԫ��
��������
��1�����ݣ�����Ʒ��������Ʒ���ۣ�1��2������Ʒ���ã�1������Ʒ���ã�11���з�����ɽ⣻
��2���ô���ϵ��������������ú�������ʽ��
��3������ȹ�ϵ�����ۼ����ۣ��������������������г����̣��ⷽ�̿ɵü��ۼۣ�
�⣺��1�������Ʒ�Ľ���ΪxԪ/��������Ʒ�Ľ���ΪyԪ/��������������
![]() �����
�����![]() ��
��
�𣺼���Ʒ�Ľ���Ϊ4Ԫ/����
��2�������Ʒÿ�����۵ļ���y���ۼ�x�亯����ϵʽΪ��y��kx+b����������ɵ�
![]() �����
�����![]() ��
��
��y��x֮��ĺ�������ʽΪ��y����20x+160��
��3�������Ʒ�ۼ۶�ΪxԪʱ�ɻ��60Ԫ���������⣬��
��x��4������20x+160����60����x2��12x+35��0��
���x1��5��x2��7��
�𣺵�����Ʒ���ۼ۶�Ϊ5Ԫ��7Ԫʱ������ʹÿ�����ۼ���Ʒ������Ϊ60Ԫ��


 ���ʿ��ÿ��ֳɳ�ϵ�д�
���ʿ��ÿ��ֳɳ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A���߶�BD�ϣ���BD��ͬ��������Rt��ABC�͵���Rt��ADE����ABC=��ADE=90�� ��CD��BE��AE�ֱ��ڵ�P��M��
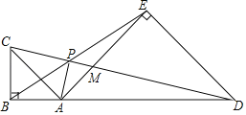
��֤����1����BAE�ס�CAD��
��2��2CB2=CPCM��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A(��4��n)��B(2����4)��һ�κ���y��kx��b�ͷ���������y��![]() ��ͼ����������㣮
��ͼ����������㣮
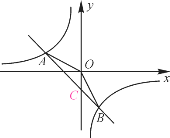
(1)��һ�κ����ͷ����������ı���ʽ��
(2)�۲�ͼ��ֱ��д������kx��b��![]() ��0�Ľ⣻
��0�Ľ⣻
(3)�۲�ͼ��ֱ��д������ʽkx��b��![]() <0�Ľ⼯��
<0�Ľ⼯��
(4)����AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+3��ͼ���� (��3��0)��(2����5)��
(1)��ȷ���˶��κ����Ľ���ʽ��
(2)�����жϵ�P(��2��3)�Ƿ���������κ�����ͼ���ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���BAD��ƽ���߽�BC�ڵ�E����DC���ӳ����ڵ�F��ȡEF���е�G������CG��BG��BD��DG�����н��ۣ�
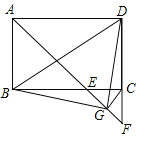
��BE=CD��
�ڡ�DGF=135����
�ۡ�ABG+��ADG=180����
����![]() ����
����![]() ��
��
������ȷ�Ľ����� ������д������ȷ���۵���ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x1��x2��һԪ���η��̣�a-6��x2+2ax+a=0������ʵ������
��1����ʵ��a��ȡֵ��Χ��
��2����x1��x2����x1x2-x1=4+ x2����ʵ��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����㹻��Ŀյ�����һ�γ�Ϊa�ľ�ǽMN��ij�����þ�ǽ��ľ��Χ��һ�����β�ABCD������AD��MN����֪���β���һ�߿�ǽ��������һ������46��ľ����
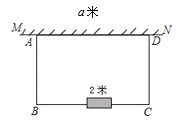
��1����a��26����Χ�ɵľ��β������Ϊ280ƽ���ף��������þ�ǽAD�ij���
��2������β�ABCD��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������ֱ���������ߣ�![]() ���룩�������ĸ߶�
���룩�������ĸ߶�![]() ���ף����ù�ʽ
���ף����ù�ʽ![]() .
.
��1����������ʱ����ĸ߶�Ϊ20�ף�
��2��С��ͬѧ˵��������߶Ȳ����ܴﵽ21�ף�������Ϊ��˵�ö�����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx����B��1����3�����Գ�����ֱ��x=2������������x��������ύ�ڵ�A��
��1���������ߵĽ���ʽ��������ͼ��ֱ��д����y��0ʱ���Ա���x��ȡֵ��ͼ��
��2���ڵڶ������ڵ�����������һ��P����PA��BAʱ������PAB�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com