练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，点A在线段BD上，在BD的同侧作等腰Rt△ABC和等腰Rt△ADE，∠ABC=∠ADE=90° ，CD与BE、AE分别交于点P、M．

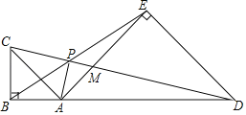
    求证：（1）△BAE∽△CAD；

    （2）2CB2=CPCM．

    【答案】（1）见解析；（2）见解析.

    【解析】

    (1)由相似三角形定理证明即可.

    （2）先证明△CAP∽△CMA，即可得AC2=CPCM，由此可得2CB2=CPCM.

    （1）证明：由已知：AC=AB，AD=AE

    ∴

    ∵∠BAC=∠EAD

    ∴∠BAE=∠CAD

    ∴△BAE∽△CAD

    （2）由（1）得到，

    ∵△BAE∽△CAD

    ∴∠BEA=∠CDA

    ∵∠PME=∠AMD

    ∴△PME∽△AMD

    ∴，

    ∴MPMD=MAME

    ∠PMA=∠DME

    ∴△PMA∽△EMD

    ∴∠APD=∠AED=90°

    ∵∠CAE=180°∠BAC∠EAD=90°

    ∴△CAP∽△CMA

    ∴AC2=CPCM

    ∵AC=AB

    ∴2CB2=CPCM

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如果三角形的两个内角α与β满足2α+β=90°，那么我们称这样的三角形为“准互余三角形”．

    （1）若△ABC是“准互余三角形”，∠C＞90°，∠A=60°，则∠B=　 　°；

    （2）如图①，在Rt△ABC中，∠ACB=90°，AC=4，BC=5．若AD是∠BAC的平分线，不难证明△ABD是“准互余三角形”．试问在边BC上是否存在点E（异于点D），使得△ABE也是“准互余三角形”？若存在，请求出BE的长；若不存在，请说明理由．

    （3）如图②，在四边形ABCD中，AB=7，CD=12，BD⊥CD，∠ABD=2∠BCD，且△ABC是“准互余三角形”，求对角线AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

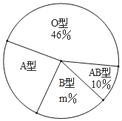
    【题目】“只要人人献出一点爱，世界将变成美好的人间”．某大学利用“世界献血日”开展自愿义务献血活动，经过检测，献血者血型有“A、B、AB、O”四种类型，随机抽取部分献血结果进行统计，根据结果制作了如图两幅不完整统计图表（表，图）：

    血型统计表

    血型

    A

    B

    AB

    O

    人数

    　 　

    10

    5

    　 　

    （1）本次随机抽取献血者人数为　 　人，图中m＝　 　；

    （2）补全表中的数据；

    （3）若这次活动中该校有1300人义务献血，估计大约有多少人是A型血？

    （4）现有4个自愿献血者，2人为O型，1人为A型，1人为B型，若在4人中随机挑选2人，利用树状图或列表法求两人血型均为O型的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

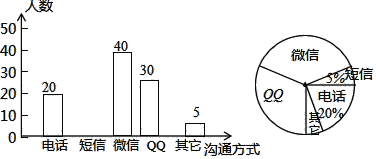
    【题目】随着通讯技术的迅猛发展，人与人之间的沟通方式更多样、便捷．某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷（每人必选且只选一种），在全校范围内随机调查了部分学生，将统计结果绘制了如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：

    （1）这次统计共抽查了　 　名学生，在扇形统计图中“QQ”的扇形圆心角的度数为　 　；

    （2）将条形统计图补充完整；

    （3）某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系，请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于x的一元二次方程x2+（2m+1）x+m2﹣1=0有两个不相等的实数根．

    （1）求m的取值范围；

    （2）写出一个满足条件的m的值，并求此时方程的根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用适当的方法解下列方程.

    （1）(2x+3)2 -16=0

    （2）3x2+x-1=0

    （3）3x(x-1)=2-2x

    （4）9(3x-1)2 =(2-x)2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是抛物线y1=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：

    ①2a+b=0；②abc＞0；③方程ax2+bx+c=3有两个相等的实数根；④抛物线与x轴的另一个交点是（﹣1，0）；⑤当1＜x＜4时，有y2＜y1，

    其中正确的是（ ）

    A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB ＝xm，花园面积S.

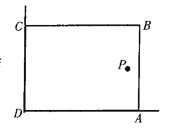
    （1）求S关于x的函数关系式，求x的取值范围；

    （2）若在P处有一棵树与墙CD，AD的距离分别是15m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），求花园面积S的最大值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某精品店购进甲、乙两种小礼品，已知1件甲礼品的进价比1件乙礼品的进价多1元，购进2件甲礼品与1件乙礼品共需11元．

    （1）求甲礼品的进价；

    （2）经市场调查发现，若甲礼品按6元/件销售，则每天可卖40件；若按5元/件销售，则每天可卖60件．假设每天销售的件数y（件）与售价x（元/件）之间满足一次函数关系，求y与x之间的函数解析式；

    （3）在（2）的条件下，当甲礼品的售价定为多少时，才能使每天销售甲礼品的利润为60元？

    查看答案和解析>>

    同步练习册答案