
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() ,与y轴交于点C,点P是抛物线上BC上方的一个动点.
,与y轴交于点C,点P是抛物线上BC上方的一个动点.
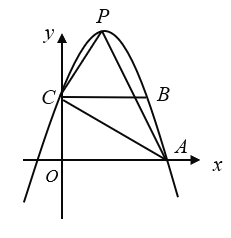
(1)求这条抛物线对应的函数表达式:
(2)当![]() PAC的面积
PAC的面积![]() 时,求点P的坐标;
时,求点P的坐标;
(3)若抛物线上有另一动点Q,满足BC平分![]() ,过点O作PQ的平行线交抛物线于点D,求点D的坐标.
,过点O作PQ的平行线交抛物线于点D,求点D的坐标.
【答案】(1)![]() ;(2)(1,4);(3)
;(2)(1,4);(3)![]() 或
或![]() .
.
【解析】
(1)将![]() ,
,![]() 代入
代入![]() ,利用待定系数法即可求出函数表达式;
,利用待定系数法即可求出函数表达式;
(2)如图1,过P作PQ⊥x轴交AC于点M,设![]() ,则
,则![]() ,
,
用代数式![]() 表示出
表示出![]() ,解方程即可得P的横坐标,从而得解;
,解方程即可得P的横坐标,从而得解;
(3)如图2,过点P分别作x轴,y轴的平行线,过Q作y轴的垂线.设![]() ,
,![]() ,由角平分线和平行线的性质得到∠CPE=∠CQF,再根据正切的定义得到
,由角平分线和平行线的性质得到∠CPE=∠CQF,再根据正切的定义得到![]() ,进而得到∠PQH的正切值,从而得出直线OD的解析式,再联立方程组求出D的坐标.
,进而得到∠PQH的正切值,从而得出直线OD的解析式,再联立方程组求出D的坐标.
(1)由题意将![]() ,
,![]() 代入
代入![]() 得:
得:
![]()
解得:![]()
![]() 抛物线的解析式为:
抛物线的解析式为:![]()
(2)如图1,过P作PQ⊥x轴交AC于点M,
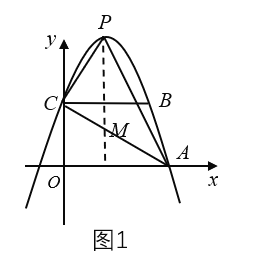
∵![]()
∴C(0,3),又A(3,0),
可得直线AC:y=-x+3,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∵![]()
解得![]() (此时点P与B重合,不合题意舍去)
(此时点P与B重合,不合题意舍去)
∴可得![]() ;
;
(3)如图2,过点P分别作x轴,y轴的平行线,过Q作y轴的垂线,
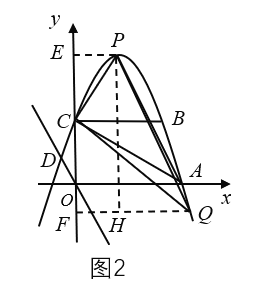
设![]() ,
,![]() .
.
由角平分线和平行线的性质得到易得∠CPE=∠CQF,
故![]() ,即:
,即:![]()
![]()
![]()
![]()
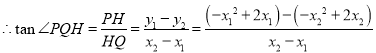
![]()
=2
![]()
可得直线OD:![]() ,
,
联立两直线得方程组:
![]()
解得: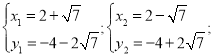
![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
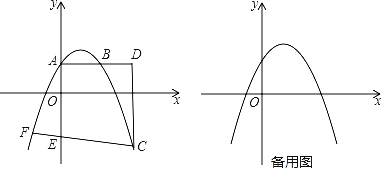
【题目】如图所示,抛物线y=ax2+bx+4的顶点坐标为(3,![]() ),与y轴交于点A.过点A作AB∥x轴,交抛物线于点B,点C是第四象限的抛物线上的一个动点,过点C作y轴的平行线,交直线AB于点D.
),与y轴交于点A.过点A作AB∥x轴,交抛物线于点B,点C是第四象限的抛物线上的一个动点,过点C作y轴的平行线,交直线AB于点D.
(1)求抛物线的函数表达式;
(2)若点E在y轴的负半轴上,且AE=AD,直线CE交抛物线y=ax2+bx+4于点F.
①求点F的坐标;
②过点D作DG⊥CE于点G,连接OD、ED,当∠ODE=∠CDG时,求直线DG的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉某超市在疫情前用3000元购进某种干果销售,发生疫情后,为了保障附近居民的生活需求,又调拨9000元购进该种干果.受疫情影响,交通等成本上涨,第二次的进价比第一次进价提高了20%,但是第二次购进干果的数量是第一次的2倍还多300千克,如果超市先按每千克9元的价格出售,当大部分干果售出后,最后的600千克按原售价的7折售完.售卖结束后,超市决定将盈利的资金捐助给武汉市用于抗击新冠肺炎疫情.那么该超市可以捐助___________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、点
、点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
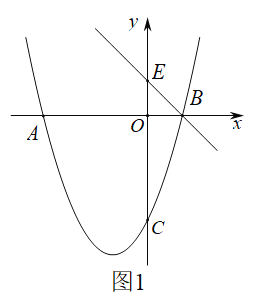
(2)如图1,点![]() 在
在![]() 轴上,连接
轴上,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
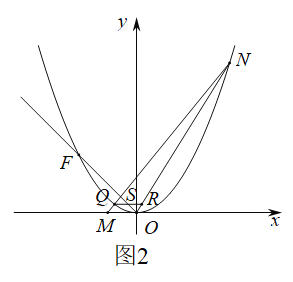
(3)如图2,将抛物线![]() 平移,使其顶点是坐标原点
平移,使其顶点是坐标原点![]() ,得到抛物线
,得到抛物线![]() ,平移直线
,平移直线![]() 经过原点
经过原点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() .点
.点![]() ,点
,点![]() 是
是![]() 第一象限内一动点,
第一象限内一动点,![]() 交
交![]() 于
于![]() 点,
点,![]() 轴分别交
轴分别交![]() 、
、![]() 于
于![]() 、
、![]() ,试探究
,试探究![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
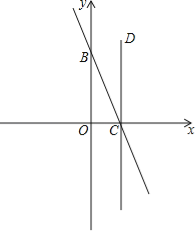
【题目】如图,直线y=-2x+4与坐标轴分别交于C、B两点,过点C作CD⊥x轴,点P是x轴下方直线CD上的一点,且△OCP与△OBC相似,求过点P的双曲线解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线与x轴交于A、B两点(点A在点B的左侧),且AB=4,顶点P(3,-4).
(1)求抛物线的解析式;
(2)若点M在抛物线上,且△MAB的面积为24,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
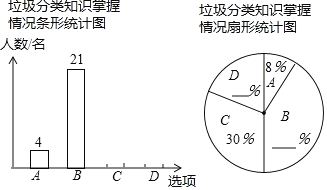
【题目】为响应市政府关于“垃圾不落地市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的掌握情况.调查选项分为“A:非常了解,B:比较了解,C:了解较少,D:不了解”四种,并将调查结果绘制成两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)把两幅统计图补充完整;
(2)若该校学生有2000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有 名;
(3)已知“非常了解”的同学有3名男生和1名女生,从中随机抽取2名进行垃圾分类的知识交流,请用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,是一款常见的海绵拖把,图2是其平面示意图,EH是拖把把手,F是把手的一个固定点,海绵安装在两片活动骨架PA,PB上,骨架的端点P只能在线段FH上移动,当海绵完全张开时,PA,PB分别与HMHN重合;当海绵闭合时,PA,PB与FH重合.已知直杆EH=120cm,FH=20cm.
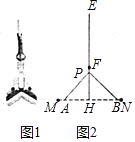
(1)若∠APB=90°,求EP的长(结果保留根号)
(2)若∠APB=26°,求MA的长(结果保留小数点后一位)
(3)海绵从完全张开到闭合的过程中,直接写出PA的中点Q运动的路径长.(参考数据:sin13°≈0.225,cos13°≈0.974,tan13°≈0.231,π取3.14)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com