
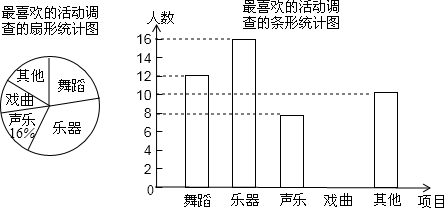
分析 (1)用喜欢声乐的人数除以所占的百分比,进行计算即可得解;
(2)用总人数减去声乐、舞蹈、乐器和其他的人数,可求出喜欢戏曲的人数,然后补全统计图即可;
(3)用其他的人数除以总人数再乘以360°,可得结果;
(4)用3100除以总人数再乘以16即可得解.
解答 解:(1)8÷16%=50(名);
(2)50-12-16-8-10=4(名),如图所示:
(3)$\frac{10}{50}×360°$=72°;
(4)$\frac{3100}{50}×16$=992(人).
故答案为:50;72;992.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:解答题
 阅读材料
阅读材料查看答案和解析>>
科目:初中数学 来源: 题型:解答题
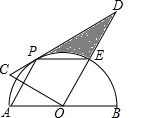 如图,在Rt△COD中,∠COD=90°,∠D=30°,斜边CD与以AB为直径,O为圆心的半圆相切于点P,OD与半圆交于点E,连接PA,PE,PA与OC交于点F.
如图,在Rt△COD中,∠COD=90°,∠D=30°,斜边CD与以AB为直径,O为圆心的半圆相切于点P,OD与半圆交于点E,连接PA,PE,PA与OC交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
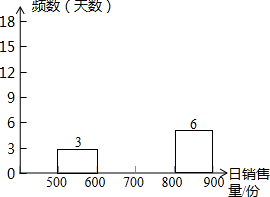 夏季来临,某饮品店老板老李计划下个月(2016年7月)每天制作新鲜水果冰激凌800份销售,去年同期,这种冰激凌每份的成本价为5元,售价为8元,该冰淇淋不含防腐剂,很受顾客的欢迎,但如果当天制作的冰淇淋未售出,新鲜水果就会腐败变质,饮品店就将承担冰淇淋制作成本的损失.根据大白去年的销售记录,得到去年同期该冰淇淋日销售量的频数分布表和频数分布直方图(不完整)如下:
夏季来临,某饮品店老板老李计划下个月(2016年7月)每天制作新鲜水果冰激凌800份销售,去年同期,这种冰激凌每份的成本价为5元,售价为8元,该冰淇淋不含防腐剂,很受顾客的欢迎,但如果当天制作的冰淇淋未售出,新鲜水果就会腐败变质,饮品店就将承担冰淇淋制作成本的损失.根据大白去年的销售记录,得到去年同期该冰淇淋日销售量的频数分布表和频数分布直方图(不完整)如下:| 日销售量分组 | 频数 |
| 500≤x<600 | 3 |
| 600≤x<700 | 6 |
| 700≤x<800 | 16 |
| 800≤x<900 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
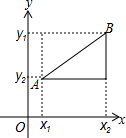
 已知:正比例函数y=ax(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点(2,2$\sqrt{2}$+2)
已知:正比例函数y=ax(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点(2,2$\sqrt{2}$+2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com