
【题目】如图,在四边形ABCD中,AD∥BC
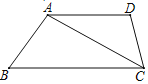
(1)作对角线AC的垂直平分线与边AD、BC分别相交于点E、F(尺规作图,保留作图痕迹,不写作法);
(2)连接AF、CE,判断四边形AFCE的形状,并说明理由.
【答案】(1)见解析;(2)四边形AFCE为菱形,见解析.
【解析】
(1)利用基本作图作EF垂直平分AC;
(2)利用线段的垂直平分线的性质得AE=CE,AF=CF,利用等腰三角形的性质得到∠AFE=∠CFE,再根据平行线的性质得∠AEF=∠CFE,所以∠AFE=∠AEF,从而得到AE=AF,然后根据菱形的判定方法可判断四边形AFCE为菱形.
解:(1)如图,点E、F为所作;
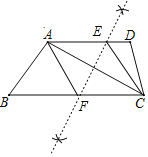
(2)四边形AFCE为菱形.理由如下:
∵EF垂直平分AC,
∴AE=CE,AF=CF,
∴EF平分∠AFC,即∠AFE=∠CFE,
∵AD∥BC,
∴∠AEF=∠CFE,
∴∠AFE=∠AEF,
∴AE=AF,
∴AE=EC=CF=AF,
∴四边形AFCE为菱形.


科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里
-4, ![]() ,
, ![]() , 0, -3.14, 717, -(+5) +1.88,
, 0, -3.14, 717, -(+5) +1.88, ![]()
(1)正有理数集合:{_____________________________…}
(2)负数集合:{_____________________________…}
(3)整数集合:{_____________________________ …}
(4)分数集合:{______________________________…}
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在做多项式乘法的时候发现,两个多项式相乘在合并同类项后的结果存在缺项的可能。比如x+2和x- 2相乘的结果为![]() , x的一次项没有了。
, x的一次项没有了。
(1)请计算![]() 与x-2相乘后的结果,并观察x的几次项没有了?
与x-2相乘后的结果,并观察x的几次项没有了?
(2)请想一下,![]() 与x+a相乘后的结果可不可能让一次项消失,如果可能,那么a应该是多少呢?
与x+a相乘后的结果可不可能让一次项消失,如果可能,那么a应该是多少呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
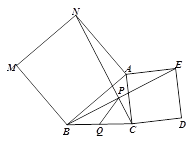
【题目】探究:如图,分别以△ABC的两边AB和AC为边向外作正方形ABMN和正方形ACDE,CN、BE交于点P. 求证:∠ANC = ∠ABE.
应用:Q是线段BC的中点,连结PQ. 若BC = 6,则PQ = ___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点坐标为A(3,4),B(2,0),C(8,0).
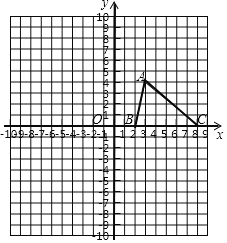
(1)请画出△ABC关于坐标原点O的中心对称图形△A′B′C′,并写出点A的对应点A′的坐标 ;
(2)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
![]()
(1)求所捂的多项式;
(2)若x为正整数,任取x的几个值并求出所捂多项式的值,你能发现什么规律?
(3)若所捂多项式的值为144,请直接写出正整数x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店购进一批甲、乙两种款型时尚T恤衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的T恤衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完 这批T恤衫商店共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
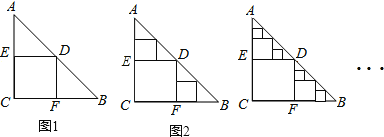
【题目】△ABC是一张等腰直角三角形纸板,∠C=Rt∠,AC=BC=2,在这张纸板中剪出一个尽可能大的正方形称为第1次剪取,记所得正方形面积为s1(如图1);在余下的Rt△ADE和Rt△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为s2(如图2);继续操作下去…;则第10次剪取时,s10= ;第2012次剪取后,余下的所有小三角形的面积之和是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对连续的偶数2,4,6,8,…排成如图的形式.若将图中的十字框上下左右移动,框住的五个数之和能等于2020吗?若能,请写出这五个数中位置在最中间的数;若不能,请说明理由.你的答案是:____________________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com