

分析 (1)由题意得出点P的坐标,从而得出答案;
(2)列表法可得所有等可能结果;
(3)根据概率公式可得答案.
解答 解:(1)若第一次骰子朝上的点数为1,第二次骰子朝上的点数为2,此时点P的坐标为(1,2),
由图可知点P落在圆O内部,
故答案为:是;
(2)列表如下:
| x y | 1 | 2 | 3 | 4 |
| 1 | (1,1) | (2,1) | (3,1) | (4,1) |
| 2 | (1,2) | (2,2) | (3,2) | (4,2) |
| 3 | (1,3) | (2,3) | (3,3) | (4,3) |
| 4 | (1,4) | (2,4) | (3,4) | (4,4) |
点评 此题将几何概率的知识和概率公式、平面直角坐标系内点的坐标特征结合起来,考查了同学们的综合应用数学知识的能力.用到的知识点为:概率=所求情况数与总情况数之比.第一象限点的符号为(+,+).


科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,-1).
如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
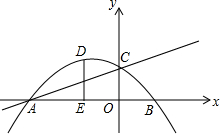 如图,抛物线y=ax2+bx+1与直线y=-ax+c相交于坐标轴上点A(-3,0),C(0,1)两点.
如图,抛物线y=ax2+bx+1与直线y=-ax+c相交于坐标轴上点A(-3,0),C(0,1)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
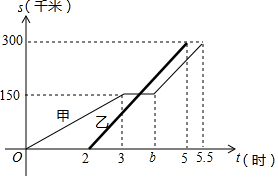 甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,设甲、乙两车与A地的路程为s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,设甲、乙两车与A地的路程为s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
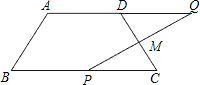 如图,在四边形ABCD中,AD∥BC,AD=5cm,BC=9cm.M是CD的中点,P是BC边上的一动点(P与B,C不重合),连接PM并延长交AD的延长线于Q.
如图,在四边形ABCD中,AD∥BC,AD=5cm,BC=9cm.M是CD的中点,P是BC边上的一动点(P与B,C不重合),连接PM并延长交AD的延长线于Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
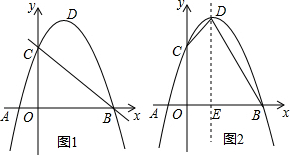 如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于点A、点B(点A在点B左侧),与y轴交于点C,点D为抛物线的顶点,已知点A、点B的坐标分别为A(-1,0)、B(3,0).
如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于点A、点B(点A在点B左侧),与y轴交于点C,点D为抛物线的顶点,已知点A、点B的坐标分别为A(-1,0)、B(3,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com