
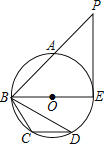
【题目】如图,已知A、B、C、D、E是⊙O上五点,⊙O的直径BE=2![]() ,∠BCD=120°,A为
,∠BCD=120°,A为![]() 的中点,延长BA到点P,使BA=AP,连接PE.
的中点,延长BA到点P,使BA=AP,连接PE.
(1)求线段BD的长;
(2)求证:直线PE是⊙O的切线.
【答案】(1)3;(2)证明见解析.
【解析】(1)连接DB,如图,利用圆内接四边形的性质得∠DEB=60°,再根据圆周角定理得到∠BDE=90°,然后根据含30度的直角三角形三边的关系计算BD的长;
(2)连接EA,如图,根据圆周角定理得到∠BAE=90°,而A为![]() 的中点,则∠ABE=45°,再根据等腰三角形的判定方法,利用BA=AP得到△BEP为等腰直角三角形,所以∠PEB=90°,然后根据切线的判定定理得到结论.
的中点,则∠ABE=45°,再根据等腰三角形的判定方法,利用BA=AP得到△BEP为等腰直角三角形,所以∠PEB=90°,然后根据切线的判定定理得到结论.
(1)连接DE,如图,
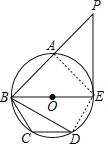
∵∠BCD+∠DEB=180°,
∴∠DEB=180°﹣120°=60°,
∵BE为直径,
∴∠BDE=90°,
在Rt△BDE中,DE=![]() BE=
BE=![]() ×2
×2![]() =
=![]() ,
,
BD=![]() DE=
DE=![]() ×
×![]() =3;
=3;
(2)证明:连接EA,如图,
∵BE为直径,
∴∠BAE=90°,
∵A为![]() 的中点,
的中点,
∴∠ABE=45°,
∵BA=AP,
而EA⊥BA,
∴△BEP为等腰直角三角形,
∴∠PEB=90°,
∴PE⊥BE,
∴直线PE是⊙O的切线.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的速度都为1cm/s.当点P到达点B时,P,Q两点停止运动,设点P的运动时间为t(s).
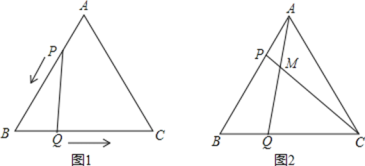
(1)当t为何值时,△PBQ是直角三角形?
(2)连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
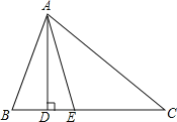
【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC
(1)若∠B=70°,∠C=30°,求;
①∠BAE的度数.
②∠DAE的度数.
(2)探究:如果只知道∠B=∠C+40°,那么能求岀∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交射线BC于点F.
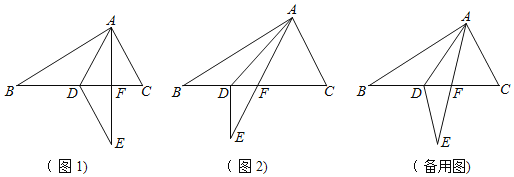
(1)如(图1),当AE⊥BC时,求证:DE∥AC
(2)若∠C=2∠B,∠BAD=x°(0<x<60)
①如(图2),当DE⊥BC时,求x的值.
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,E、F分别为线段AB、AC上的点(不与A、B、C重合).
(1)如图1,若EF∥BC,求证:![]()
(2)如图2,若EF不与BC平行,(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若EF上一点G恰为△ABC的重心,![]() ,求
,求![]() 的值.
的值.
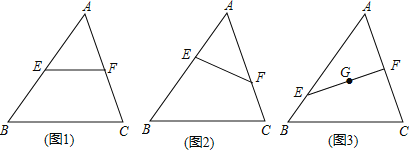
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:
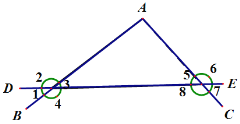
(1)∠A和∠5是直线______和直线_____被直线_______所截而成的,∠A和∠4是直线_____和直线_____被直线_____所截而成的,∠1和∠8是直线_____和直线_____被直线___________所截而成的.
(2)指出图中所有的同位角__________,________________;指出图中所有的内错角_______,________________;
查看答案和解析>>
科目:初中数学 来源: 题型:
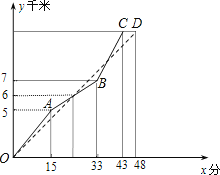
【题目】如图表示甲、乙两名选手在一次自行车越野赛中,路程y(千米)随时间x(分)变化的图象.下面几个结论:①比赛开始24分钟时,两人第一次相遇.②这次比赛全程是10千米.③比赛开始38分钟时,两人第二次相遇.正确的结论为_____(只填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
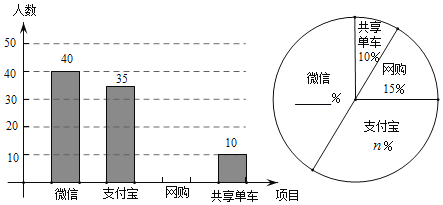
(1)根据图中信息求出m= ,n= ;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
(4)已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com