
【题目】如图:
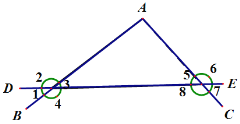
(1)∠A和∠5是直线______和直线_____被直线_______所截而成的,∠A和∠4是直线_____和直线_____被直线_____所截而成的,∠1和∠8是直线_____和直线_____被直线___________所截而成的.
(2)指出图中所有的同位角__________,________________;指出图中所有的内错角_______,________________;
科目:初中数学 来源: 题型:
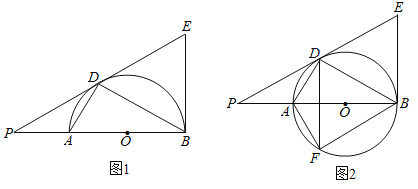
【题目】如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD交圆的切线BE于点E
(1)证明:直线PD是⊙O的切线.
(2)如果∠BED=60°,![]() ,求PA的长.
,求PA的长.
(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
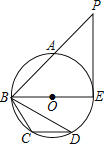
【题目】如图,已知A、B、C、D、E是⊙O上五点,⊙O的直径BE=2![]() ,∠BCD=120°,A为
,∠BCD=120°,A为![]() 的中点,延长BA到点P,使BA=AP,连接PE.
的中点,延长BA到点P,使BA=AP,连接PE.
(1)求线段BD的长;
(2)求证:直线PE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x﹣1)2过点(3,1),D为抛物线的顶点.
(1)求抛物线的解析式;
(2)若点B、C均在抛物线上,其中点B(0,![]() ),且∠BDC=90°,求点C的坐标;
),且∠BDC=90°,求点C的坐标;
(3)如图,直线y=kx+4﹣k与抛物线交于P、Q两点.
①求证:∠PDQ=90°;
②求△PDQ面积的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图形,回答下列各题:
(1)图A中,共有____对对顶角;
(2)图B中,共有____对对顶角;
(3)图C中,共有____对对顶角;
(4)探究(1)--(3)各题中直线条数与对顶角对数之间的关系,若有n条直线相交于一点,则可形成________对对顶角;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某学校的教室多媒体投影仪E正对投影幕布AB的中央,其距离EG = 3.60米.为了方便课堂教学与使用,现将投影幕布由黑板正中AB的位置调整到左面BC的位置处,测得![]() 米,
米,![]() ,此时投影仪E调整到线段EB上的点F处且恰好正对投影幕布BC的中央.若投影仪与投影幕布的安装距离控制在3.45米到3.65米之间效果最好,则调整后的投影仪F与投影幕布BC之间的距离是否符合要求?请通过计算加以说明.
,此时投影仪E调整到线段EB上的点F处且恰好正对投影幕布BC的中央.若投影仪与投影幕布的安装距离控制在3.45米到3.65米之间效果最好,则调整后的投影仪F与投影幕布BC之间的距离是否符合要求?请通过计算加以说明.
(参考数据:![]()
![]()
![]() ,结果精确到0.01)
,结果精确到0.01)

查看答案和解析>>
科目:初中数学 来源: 题型:
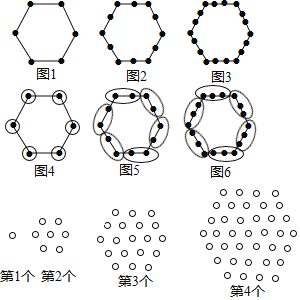
【题目】“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.
例如:图1有6个点,图2有12个点,图3有18个点,……,按此规律,求图10、图n有多少个点?
我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图),这样图1中黑点个数是6×1=6个;图2中黑点个数是6×2=12个:图3中黑点个数是6×3=18个;所以容易求出图10、图n中黑点的个数分别是 、 .
请你参考以上“分块计数法”,先将下面的点阵进行分块(画在答题卡上),再完成以下问题:
(1)第5个点阵中有 个圆圈;第n个点阵中有 个圆圈.
(2)小圆圈的个数会等于271吗?如果会,请求出是第几个点阵.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com