
【题目】已知抛物线y=a(x﹣1)2过点(3,1),D为抛物线的顶点.
(1)求抛物线的解析式;
(2)若点B、C均在抛物线上,其中点B(0,![]() ),且∠BDC=90°,求点C的坐标;
),且∠BDC=90°,求点C的坐标;
(3)如图,直线y=kx+4﹣k与抛物线交于P、Q两点.
①求证:∠PDQ=90°;
②求△PDQ面积的最小值.

【答案】(1)y=![]() (x﹣1)2;(2)点C的坐标为(17,64).(3)①证明见解析;②16.
(x﹣1)2;(2)点C的坐标为(17,64).(3)①证明见解析;②16.
【解析】(1)将点(3,1)代入解析式求得a的值即可;
(2)设点C的坐标为(x0,y0),其中y0=![]() (x0﹣1)2,作CF⊥x轴,证△BDO∽△DCF得
(x0﹣1)2,作CF⊥x轴,证△BDO∽△DCF得![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() 据此求得x0的值即可得;
据此求得x0的值即可得;
(3)①设点P的坐标为(x1,y1),点Q为(x2,y2),联立直线和抛物线解析式,化为关于x的方程可得![]() ,据此知(x1﹣1)(x2﹣1)=﹣16,由PM=y1=
,据此知(x1﹣1)(x2﹣1)=﹣16,由PM=y1=![]() (x1﹣1)2、QN=y2=
(x1﹣1)2、QN=y2=![]() (x2﹣1)2、DM=|x1﹣1|=1﹣x1、DN=|x2﹣1|=x2﹣1知PMQN=DMDN=16,即
(x2﹣1)2、DM=|x1﹣1|=1﹣x1、DN=|x2﹣1|=x2﹣1知PMQN=DMDN=16,即![]() =
=![]() ,从而得△PMD∽△DNQ,据此进一步求解可得;
,从而得△PMD∽△DNQ,据此进一步求解可得;
②过点D作x轴的垂线交直线PQ于点G,则DG=4,根据S△PDQ=![]() DGMN列出关于k的等式求解可得.
DGMN列出关于k的等式求解可得.
(1)将点(3,1)代入解析式,得:4a=1,
解得:a=![]() ,
,
所以抛物线解析式为y=![]() (x﹣1)2;
(x﹣1)2;
(2)由(1)知点D坐标为(1,0),
设点C的坐标为(x0,y0),(x0>1、y0>0),
则y0=![]() (x0﹣1)2,
(x0﹣1)2,
如图1,过点C作CF⊥x轴,
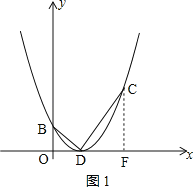
∴∠BOD=∠DFC=90°、∠DCF+∠CDF=90°,
∵∠BDC=90°,
∴∠BDO+∠CDF=90°,
∴∠BDO=∠DCF,
∴△BDO∽△DCF,
∴![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
解得:x0=17,此时y0=64,
∴点C的坐标为(17,64).
(3)①证明:设点P的坐标为(x1,y1),点Q为(x2,y2),(其中x1<1<x2,y1>0,y2>0),
由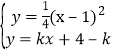 ,得:x2﹣(4k+2)x+4k﹣15=0,
,得:x2﹣(4k+2)x+4k﹣15=0,
∴![]() ,
,
∴(x1﹣1)(x2﹣1)=﹣16,
如图2,分别过点P、Q作x轴的垂线,垂足分别为M、N,
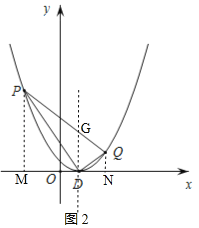
则PM=y1=![]() (x1﹣1)2,QN=y2=
(x1﹣1)2,QN=y2=![]() (x2﹣1)2,
(x2﹣1)2,
DM=|x1﹣1|=1﹣x1、DN=|x2﹣1|=x2﹣1,
∴PMQN=DMDN=16,
∴![]() =
=![]() ,
,
又∠PMD=∠DNQ=90°,
∴△PMD∽△DNQ,
∴∠MPD=∠NDQ,
而∠MPD+∠MDP=90°,
∴∠MDP+∠NDQ=90°,即∠PDQ=90°;
②过点D作x轴的垂线交直线PQ于点G,则点G的坐标为(1,4),
所以DG=4,
∴S△PDQ=![]() DGMN=
DGMN=![]() ×4×|x1﹣x2|=2
×4×|x1﹣x2|=2![]() =8
=8![]() ,
,
∴当k=0时,S△PDQ取得最小值16.


科目:初中数学 来源: 题型:
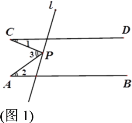
【题目】已知直线AB∥CD,点P为直线l上一点,尝试探究并解答:
(1)如图1,若点P在两平行线之间,∠1=23°,∠2=35°,则∠3= ;
(2)探究图1中∠1,∠2与∠3之间的数量关系,并说明理由;
(3)如图2,若点P在CD的上方,探究∠1,∠2与∠3之间有怎样的数量关系,并说明理由;
(4)如图3,若∠PCD与∠PAB的平分线交于点P1,∠DCP1与∠BAP1的平分线交于点P2,∠DCP2与∠BAP2的平分线交于点P3,…,∠DCPn-1与∠BAPn-1的平分线交于点Pn,若∠PCD=α,∠PAB=β,直接写出∠APnC的度数(用含α与β的代数式表示).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交射线BC于点F.
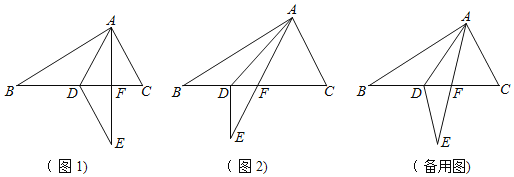
(1)如(图1),当AE⊥BC时,求证:DE∥AC
(2)若∠C=2∠B,∠BAD=x°(0<x<60)
①如(图2),当DE⊥BC时,求x的值.
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
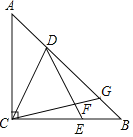
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别在边AB、CB上,CD=DE,∠CDB=∠DEC,过点C作CF⊥DE于点F,交AB于点G,
(1)求证:△ACD≌△BDE;
(2)求证:△CDG为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:
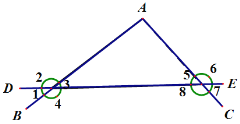
(1)∠A和∠5是直线______和直线_____被直线_______所截而成的,∠A和∠4是直线_____和直线_____被直线_____所截而成的,∠1和∠8是直线_____和直线_____被直线___________所截而成的.
(2)指出图中所有的同位角__________,________________;指出图中所有的内错角_______,________________;
查看答案和解析>>
科目:初中数学 来源: 题型:
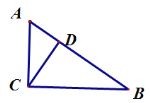
【题目】如图,已知AC⊥BC于C,CD⊥AB于D,BC=8,AC=6,CD=4.8,BD=6.4,AD=3.6.则:
(1)点A到直线CD的距离为_________;
(2)点A到直线BC的距离为_________;
(3)点B到直线CD的距离为_________;
(4)点B到直线AC的距离为_________;
(5)点C到直线AB的距离为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
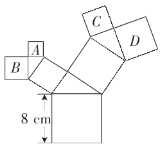
【题目】如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为8 cm,正方形A的面积是10cm2,B的面积是11 cm2,C的面积是13 cm2,则D的面积为____cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为引导学生“爱读书,多读书,读好书”,某校七(2)班决定购买A、B两种书籍.若购买A种书籍1本和B种书籍3本,共需要180元;若购买A种书籍3本和B种书籍1本,共需要140元.
(1)求A、B两种书籍每本各需多少元?
(2)该班根据实际情况,要求购买A、B两种书籍总费用不超过700元,并且购买B种书籍的数量是A种书籍的![]() ,求该班本次购买A、B两种书籍有哪几种方案?
,求该班本次购买A、B两种书籍有哪几种方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com