
【题目】如图,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,点
,点![]() 在
在![]() 上,求证:
上,求证:![]() .
.
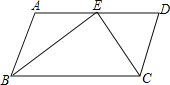
【答案】详见解析
【解析】
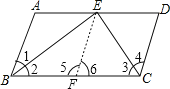
在BC上取点F,使BF=BA,连接EF,由角平分线的性质可以得出∠1=∠2,从而可以得出△ABE≌△FBE,可以得出∠A=∠5,进而可以得出△CDE≌△CFE,就可以得出CD=CF,即可得出结论.
在BC上取点F,使BF=BA,连接EF,
∵BE、CE分别是∠ABC和∠BCD的平分线,
∴∠1=∠2,∠3=∠4,
在△ABE和△FBE中,
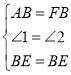 ,
,
∴△ABE≌△FBE(SAS),
∴∠A=∠5,
∵AB∥CD,
∴∠A+∠D=180°,
∴∠5+∠D=180,
∵∠5+∠6=180°,
∴∠6=∠D,
在△CDE和△CFE中,
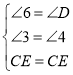 ,
,
∴△CDE≌△CFE(AAS),
∴CF=CD.
∵BC=BF+CF,
∴BC=AB+CD.


科目:初中数学 来源: 题型:
【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球.B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC
(1)若∠B=70°,∠C=30°,求;
①∠BAE的度数.
②∠DAE的度数.
(2)探究:如果只知道∠B=∠C+40°,那么能求岀∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
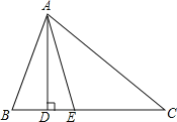
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD,点P为直线l上一点,尝试探究并解答:
(1)如图1,若点P在两平行线之间,∠1=23°,∠2=35°,则∠3= ;
(2)探究图1中∠1,∠2与∠3之间的数量关系,并说明理由;
(3)如图2,若点P在CD的上方,探究∠1,∠2与∠3之间有怎样的数量关系,并说明理由;
(4)如图3,若∠PCD与∠PAB的平分线交于点P1,∠DCP1与∠BAP1的平分线交于点P2,∠DCP2与∠BAP2的平分线交于点P3,…,∠DCPn-1与∠BAPn-1的平分线交于点Pn,若∠PCD=α,∠PAB=β,直接写出∠APnC的度数(用含α与β的代数式表示).
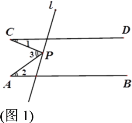


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交射线BC于点F.
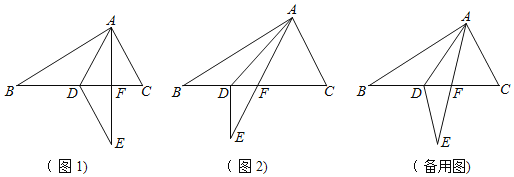
(1)如(图1),当AE⊥BC时,求证:DE∥AC
(2)若∠C=2∠B,∠BAD=x°(0<x<60)
①如(图2),当DE⊥BC时,求x的值.
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:
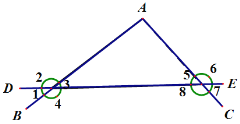
(1)∠A和∠5是直线______和直线_____被直线_______所截而成的,∠A和∠4是直线_____和直线_____被直线_____所截而成的,∠1和∠8是直线_____和直线_____被直线___________所截而成的.
(2)指出图中所有的同位角__________,________________;指出图中所有的内错角_______,________________;
查看答案和解析>>
科目:初中数学 来源: 题型:
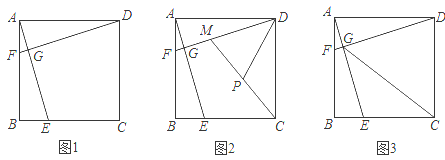
【题目】如图1,在正方形ABCD中,E、F分别是BC、AB上一点,且AF=BE,AE与DF交于点G.
(1)求证:AE=DF.
(2)如图2,在DG上取一点M,使AG=MG,连接CM,取CM的中点P.写出线段PD与DG之间的数量关系,并说明理由.
(3)如图3,连接CG.若CG=BC,则AF:FB的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com