
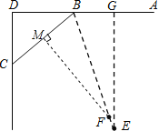
【题目】如图,某学校的教室多媒体投影仪E正对投影幕布AB的中央,其距离EG = 3.60米.为了方便课堂教学与使用,现将投影幕布由黑板正中AB的位置调整到左面BC的位置处,测得![]() 米,
米,![]() ,此时投影仪E调整到线段EB上的点F处且恰好正对投影幕布BC的中央.若投影仪与投影幕布的安装距离控制在3.45米到3.65米之间效果最好,则调整后的投影仪F与投影幕布BC之间的距离是否符合要求?请通过计算加以说明.
,此时投影仪E调整到线段EB上的点F处且恰好正对投影幕布BC的中央.若投影仪与投影幕布的安装距离控制在3.45米到3.65米之间效果最好,则调整后的投影仪F与投影幕布BC之间的距离是否符合要求?请通过计算加以说明.
(参考数据:![]()
![]()
![]() ,结果精确到0.01)
,结果精确到0.01)

【答案】调整后的投影仪F与投影幕布BC之间的距离符合要求.
【解析】过点F作FM⊥BD于点M.由已知可得BG,BM,先根据正切求∠GBE,再求∠FBM,在Rt△FBM中,由tan∠FBM=![]() ,可求得答案.
,可求得答案.
解:过点F作FM⊥BD于点M.则有M为BC的中点,
即BM=![]() BD=1.3m.
BD=1.3m.
又据题意知EG垂直平分AB,
则BG=![]() AB=1.3m,而EG=3.60m,
AB=1.3m,而EG=3.60m,
在Rt△EBG中,tan∠GBE=![]() ≈2.770,
≈2.770,
∠GBE≈70.15°.
又∵∠DBC=39.85°,
∴∠FBM=180°-70.15°-39.85°=70°.
因而,在Rt△FBM中,∵tan∠FBM=![]() ,
,
∴FM=BMtan70°≈1.3×2.747≈3.57(米).
∵3.45<3.57<3.65,
∴调整后的投影仪F与投影幕布BD之间的距离符合要求.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
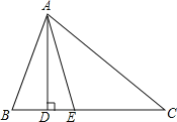
【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC
(1)若∠B=70°,∠C=30°,求;
①∠BAE的度数.
②∠DAE的度数.
(2)探究:如果只知道∠B=∠C+40°,那么能求岀∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:
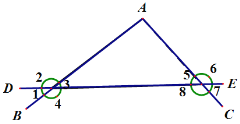
(1)∠A和∠5是直线______和直线_____被直线_______所截而成的,∠A和∠4是直线_____和直线_____被直线_____所截而成的,∠1和∠8是直线_____和直线_____被直线___________所截而成的.
(2)指出图中所有的同位角__________,________________;指出图中所有的内错角_______,________________;
查看答案和解析>>
科目:初中数学 来源: 题型:
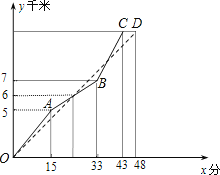
【题目】如图表示甲、乙两名选手在一次自行车越野赛中,路程y(千米)随时间x(分)变化的图象.下面几个结论:①比赛开始24分钟时,两人第一次相遇.②这次比赛全程是10千米.③比赛开始38分钟时,两人第二次相遇.正确的结论为_____(只填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为8 cm,正方形A的面积是10cm2,B的面积是11 cm2,C的面积是13 cm2,则D的面积为____cm2.
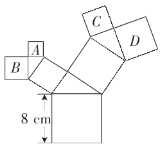
查看答案和解析>>
科目:初中数学 来源: 题型:
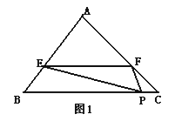
【题目】如图1,某人用一张面积为S的三角形纸片ABC剪出一个△EFP,记△EFP的面积为T,已知E、F、P分别是△ABC三边上的三点,且EF∥BC.
(1)如图2,当P与B重合,设![]() 分别等于
分别等于![]() 、
、![]() 、
、![]() 时,△PEF的面积分别为
时,△PEF的面积分别为![]() 、
、![]() 、
、![]() .
.
① ![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
② 写出![]() 的求解过程;
的求解过程;
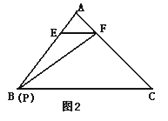
(2)如图3,当点P是△ABC边BC上的任意一点时(点P可与B或C重合),设![]() , 试求出
, 试求出![]() 与
与![]() 、S的函数关系式;
、S的函数关系式;
(3)请探究T是否存在最大值,若存在,请求出这个最大值;若不存在,请说明理由.
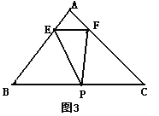
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,E、F分别是BC、AB上一点,且AF=BE,AE与DF交于点G.
(1)求证:AE=DF.
(2)如图2,在DG上取一点M,使AG=MG,连接CM,取CM的中点P.写出线段PD与DG之间的数量关系,并说明理由.
(3)如图3,连接CG.若CG=BC,则AF:FB的值为 .
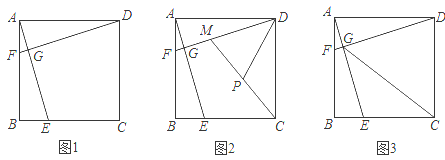
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
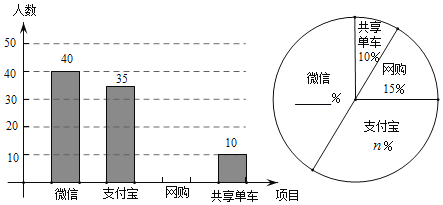
(1)根据图中信息求出m= ,n= ;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
(4)已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com