
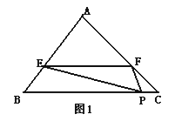
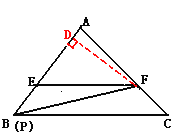
【题目】如图1,某人用一张面积为S的三角形纸片ABC剪出一个△EFP,记△EFP的面积为T,已知E、F、P分别是△ABC三边上的三点,且EF∥BC.
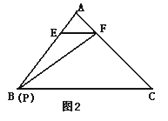
(1)如图2,当P与B重合,设![]() 分别等于
分别等于![]() 、
、![]() 、
、![]() 时,△PEF的面积分别为
时,△PEF的面积分别为![]() 、
、![]() 、
、![]() .
.
① ![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
② 写出![]() 的求解过程;
的求解过程;
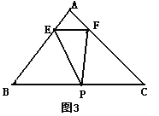
(2)如图3,当点P是△ABC边BC上的任意一点时(点P可与B或C重合),设![]() , 试求出
, 试求出![]() 与
与![]() 、S的函数关系式;
、S的函数关系式;
(3)请探究T是否存在最大值,若存在,请求出这个最大值;若不存在,请说明理由.
【答案】(1)①![]() S,
S,![]() ,
,![]() ;②见解析;(2)
;②见解析;(2)![]() ,理由见解析;(3)T存在最大值,当k=
,理由见解析;(3)T存在最大值,当k=![]() 时,
时,![]() .
.
【解析】(1)由等高可推出面积比等于底边之比,进而推出三角形面积;
(2)点P在BC上的任意一处,连BF,由EF∥BC,得△BEF与![]() 同高等底,因此
同高等底,因此![]() ,由(1)可知:△AEF∽△ABC,可得
,由(1)可知:△AEF∽△ABC,可得![]() ︰S=
︰S=![]() ︰1,即
︰1,即![]() =S·
=S·![]() ,
,
由AE︰AB=k︰1,得AE︰BE=k︰(1-k),故![]() ︰
︰![]() =k︰(1-k),即k·
=k︰(1-k),即k·![]() =(1-k)·
=(1-k)·![]() ,所以k︰T=((1-k)
,所以k︰T=((1-k)![]() S,化简可得.
S,化简可得.
(3) 由(2)可知T=-(![]() -k)S,求抛物线的顶点坐标可得.
-k)S,求抛物线的顶点坐标可得.
解:(1)①![]() =
=![]() S,
S,![]() =
=![]() ,
,![]() =
=![]() S;
S;
②如图∵EF∥BC,
∴∠AEF=∠ABC,∠A=∠A,
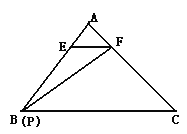
∴△AEF∽△ABC,
又∵![]() ,
,
∴![]() ,
,
∴![]() =
=![]() S.过F作FD⊥AB于D,
S.过F作FD⊥AB于D,
∵![]() FD·BE,
FD·BE,![]() ,
,
由于AE︰AB=3︰4,
∴AE︰BE=3︰1,
∴![]() ,
,
∴![]() =
=![]() ,
,![]() =
=![]() S.
S.
(2)当![]() 时,
时,![]() ,理由如下:
,理由如下:
如图,点P在BC上的任意一处,连BF,
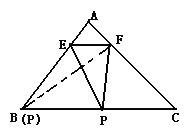
∴EF∥BC,△BEF与![]() 同高等底,
同高等底,
∴![]() ,
,
由(1)可知:△AEF∽△ABC,
设AE︰AB=k︰1,
![]() ︰S=
︰S=![]() ︰1,
︰1,
∴![]() =S·
=S·![]() .
.
又∵AE︰AB=k︰1,则AE︰BE=k︰(1-k),
![]() ︰
︰![]() =k︰(1-k),k·
=k︰(1-k),k·![]() =(1-k)·
=(1-k)·![]() ,k︰T=((1-k)
,k︰T=((1-k)![]() S
S
T=(1-k)kS即T=-(![]() -k)S;
-k)S;
(3)由(2)可知T=-(![]() -k)S=-(
-k)S=-(![]() -k+
-k+![]() -
-![]() )S=-S(k-
)S=-S(k-![]() )
)![]() +
+![]() ,
,
∴T存在最大值,当k=![]() 时,
时,![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】(1)(发现)如图①,已知等边△ABC,将直角三角板的60°角顶点D任意放在BC边上(点D不与点B、C重合),使两边分别交线段AB、AC于点E、F.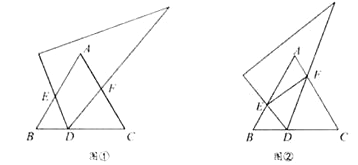
①若AB=6,AE=4,BD=2,则CF =________;
②求证:△EBD∽△DCF.
(2)(思考)若将图①中的三角板的顶点D在BC边上移动,保持三角板与边AB、AC的两个交点E、F都存在,连接EF,如图②所示.问点D是否存在某一位置,使ED平分∠BEF且FD平分∠CFE?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)(探索)如图③,在等腰△ABC中,AB=AC,点O为BC边的中点,将三角形透明纸板的一个顶点放在点O处(其中∠MON=∠B),使两条边分别交边AB、AC于点E、F(点E、F均不与△ABC的顶点重合),连接EF.设∠B=α,则△AEF与△ABC的周长之比为________(用含α的表达式表示)
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+4与x轴、y轴分别交于点A、B、C是线段AB上一点,四边形OADC是菱形,则OD的长为( )
x+4与x轴、y轴分别交于点A、B、C是线段AB上一点,四边形OADC是菱形,则OD的长为( )
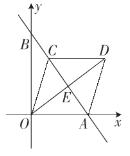
A. 4.2B. 4.8C. 5.4D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某学校的教室多媒体投影仪E正对投影幕布AB的中央,其距离EG = 3.60米.为了方便课堂教学与使用,现将投影幕布由黑板正中AB的位置调整到左面BC的位置处,测得![]() 米,
米,![]() ,此时投影仪E调整到线段EB上的点F处且恰好正对投影幕布BC的中央.若投影仪与投影幕布的安装距离控制在3.45米到3.65米之间效果最好,则调整后的投影仪F与投影幕布BC之间的距离是否符合要求?请通过计算加以说明.
,此时投影仪E调整到线段EB上的点F处且恰好正对投影幕布BC的中央.若投影仪与投影幕布的安装距离控制在3.45米到3.65米之间效果最好,则调整后的投影仪F与投影幕布BC之间的距离是否符合要求?请通过计算加以说明.
(参考数据:![]()
![]()
![]() ,结果精确到0.01)
,结果精确到0.01)

查看答案和解析>>
科目:初中数学 来源: 题型:
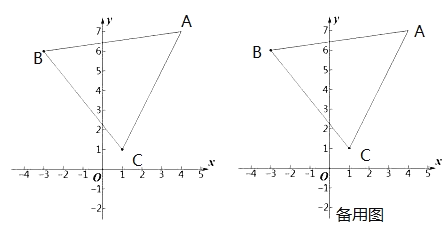
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() 其中
其中![]() 满足:
满足:![]() .
.
(1)![]()
(2)在坐标平面内,将△ABC平移,点A的对应点为点D,点B的对应点为点E,点C的对应点为点F,若平移后E、F两点都在坐标轴上,请直接写出点E的坐标;
(3)若在△ABC内部的![]() 轴上存在一点P,在(2)的平移下,点P的对应点为点Q,使得△APQ的面积为10,则点P的坐标为_________.
轴上存在一点P,在(2)的平移下,点P的对应点为点Q,使得△APQ的面积为10,则点P的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
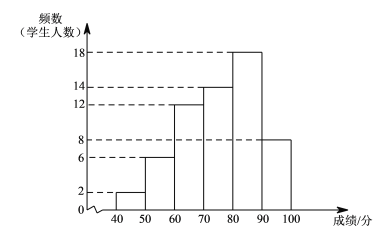
【题目】某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
![]() .A课程成绩的频数分布直方图如下(数据分成6组:
.A课程成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
![]() .A课程成绩在
.A课程成绩在![]() 这一组是:
这一组是:
70 71 71 71 76 76 77 78 ![]()
![]() 79 79 79
79 79 79 ![]()
![]() .A,B两门课程成绩的平均数、中位数、众数如下:
.A,B两门课程成绩的平均数、中位数、众数如下:
课程 | 平均数 | 中位数 | 众数 |
A |
|
|
|
B |
| 70 | 83 |
根据以上信息,回答下列问题:
(1)写出表中![]() 的值;
的值;
(2)在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是________(填“A”或“B”),理由是_______;
(3)假设该年级学生都参加此次测试,估计A课程成绩超过![]() 分的人数.
分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
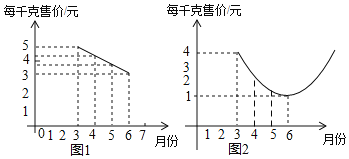
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com