
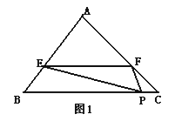
【题目】(1)(发现)如图①,已知等边△ABC,将直角三角板的60°角顶点D任意放在BC边上(点D不与点B、C重合),使两边分别交线段AB、AC于点E、F.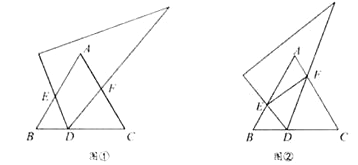
①若AB=6,AE=4,BD=2,则CF =________;
②求证:△EBD∽△DCF.
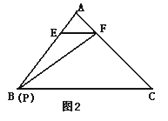
(2)(思考)若将图①中的三角板的顶点D在BC边上移动,保持三角板与边AB、AC的两个交点E、F都存在,连接EF,如图②所示.问点D是否存在某一位置,使ED平分∠BEF且FD平分∠CFE?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
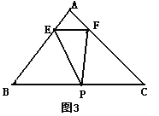
(3)(探索)如图③,在等腰△ABC中,AB=AC,点O为BC边的中点,将三角形透明纸板的一个顶点放在点O处(其中∠MON=∠B),使两条边分别交边AB、AC于点E、F(点E、F均不与△ABC的顶点重合),连接EF.设∠B=α,则△AEF与△ABC的周长之比为________(用含α的表达式表示)
.
【答案】(1)①4;②证明见解析;(2)存在;(3)1-cosα.
【解析】(1)①先求出BE的长度后发现BE=BD,又∠B=60°,可知△BDE是等边三角形,可得∠BDE=60°,另外∠EDF=60°,可证得△CDF是等边三角形,从而CF=CD=BC-BD;
②证明△EBD∽△DCF,这个模型可称为“一线三等角相似模型”,根据“AA”判定相似;
(2)【思考】由平分线可联系到角平分线的性质“角平分线上的点到角两边的距离相等”,可过D作DM⊥BE,DG⊥EF,DN⊥CF,则DM=DG=DN,从而通过证明△BDM△CDN可得BD=CD;
(3)【探索】由已知不难求得C△ABC=AB+BC+CA=2AB+2OB=2(m+mcosα),则需要用m和α的三角函数表示出C△AEF,C△AEF=AE+EF+AF;题中直接已知O是BC的中点,应用(2)题的方法和结论,作OG⊥BE,OD⊥EF,OH⊥CF,可得EG=ED,FH=DF,则C△AEF=AE+EF+AF= AG+AH=2AG,而AG=AB-OB,从而可求得.
(1)①∵△ABC是等边三角形,
∴AB=BC=AC=6,∠B=∠C=60°,
∵AE=4,
∴BE=2,则BE=BD,
∴△BDE是等边三角形,
∴∠BDE=60°,
又∵∠EDF=60°,
∴∠CDF=180°-∠EDF-∠B=60°,则∠CDF =∠C=60°,
∴△CDF是等边三角形,
∴CF=CD=BC-BD=6-2=4;
②证明:∵∠EDF=60°,∠B=60°
∴∠CDF+∠BDE=120°,∠BED+∠BDE=120°,
∴∠BED=∠CDF,
又∵∠B=∠C,
∴△EBD∽△DCF
(2)存在.如图,作DM⊥BE,DG⊥EF,DN⊥CF,垂足分别为M,G,N,
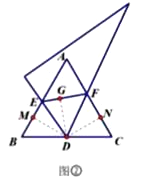
∵ED平分∠BEF且FD平分∠CFE,
∴DM=DG=DN,
又∵∠B=∠C=60°,∠BMD=∠CND=90°,
∴△BDM△CDN,
∴BD=CD,
即点D是BC的中点,
∴![]() ;
;
( 3 )连结AO,作OG⊥BE,OD⊥EF,OH⊥CF,垂足分别为G,D,H,
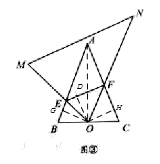
则∠BGO=∠CHO=90°,
∵AB=AC,O是BC的中点
∴∠B=∠C,OB=OC,
∴△OBG△OCH,
∴OG=OH,GB=CH,∠BOG=∠COH=90°α,
则∠GOH=180°-(∠BOG+∠COH)=2α,
∵∠EOF=∠B=α,
则∠GOH=2∠EOF=2α,
由(2)题可猜想应用EF=ED+DF=EG+FH,
则 C△AEF=AE+EF+AF=AE+EG+FH+AF=AG+AH=2AG,
设AB=m,则OB=mcosα,GB=mcos2α,
![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
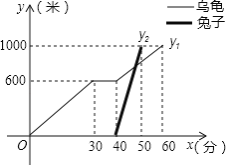
①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只跳蚤在第一象限及x轴、y轴上跳动,第一秒它从原点跳动到点(0,1),第二秒它从点(0,1)跳到点(1,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],每秒跳动一个单位长度,那么30秒后跳蚤所在位置的坐标是___.
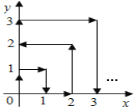
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. 20 B. 25 C. 30 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC
(1)若∠B=70°,∠C=30°,求;
①∠BAE的度数.
②∠DAE的度数.
(2)探究:如果只知道∠B=∠C+40°,那么能求岀∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
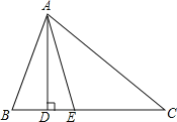
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课本中,有这样一道题:已知:如(图1),∠B+∠C=∠BEC求证:AB∥CD
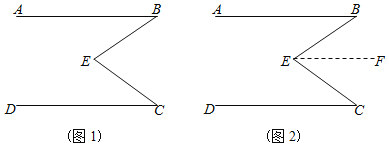
(1)请补充下面证明过程
证明:过点E,做EF∥AB,如(图2)
∴∠B=∠
∵∠B+∠C=∠BEC∠BEF+∠FEC=∠BEC(已知)
∴∠B+∠C=∠BEF+∠FEC(等量代换)
∴∠ =∠ (等式性质)
∴EF∥
∵EF∥AB
∴AB∥CD(平行于同一条直线的两条直线互相平行)
(2)请再选用一种方法,加以证明
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,E、F分别为线段AB、AC上的点(不与A、B、C重合).
(1)如图1,若EF∥BC,求证:![]()
(2)如图2,若EF不与BC平行,(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若EF上一点G恰为△ABC的重心,![]() ,求
,求![]() 的值.
的值.
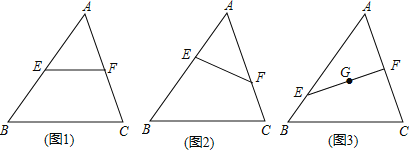
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某人用一张面积为S的三角形纸片ABC剪出一个△EFP,记△EFP的面积为T,已知E、F、P分别是△ABC三边上的三点,且EF∥BC.
(1)如图2,当P与B重合,设![]() 分别等于
分别等于![]() 、
、![]() 、
、![]() 时,△PEF的面积分别为
时,△PEF的面积分别为![]() 、
、![]() 、
、![]() .
.
① ![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
② 写出![]() 的求解过程;
的求解过程;
(2)如图3,当点P是△ABC边BC上的任意一点时(点P可与B或C重合),设![]() , 试求出
, 试求出![]() 与
与![]() 、S的函数关系式;
、S的函数关系式;
(3)请探究T是否存在最大值,若存在,请求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com