
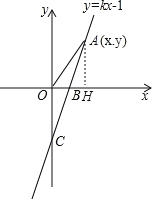
【题目】如图,直线y=kx-1与x轴、y轴分别交于B、C两点,OB:OC=![]() .
.
(1)求B点的坐标和k的值.
(2)若点A(x,y)是第一象限内的直线y=kx-1上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;
(3)在(2)的条件下,当点A运动到什么位置时,△AOB的面积是![]() .
.

【答案】(1)B(![]() ,0),OB=
,0),OB=![]() (2)S=
(2)S= ![]()
![]() ,(x>
,(x>![]() ) (3)A(
) (3)A(![]() ,
,![]() )
)
【解析】
(1)可先求出OC长,并用k的代数式表示点B的坐标及OB的长,然后在△BOC中运用三角函数可求出∠OCB的度数,再运用三角函数就可解决问题.
(2)过点A作AH⊥x轴于H,由于点A在直线y=kx-1上,因此可用x的代数式表示y,进而可得到S与x的函数关系式.
(3)把S=![]() 代入(2)中的解析式就可得到点A的横坐标,进而可得到点A的纵坐标.
代入(2)中的解析式就可得到点A的横坐标,进而可得到点A的纵坐标.
(1)在Rt△BOC中,
∵![]() =0,
=0,
∴k![]() 1=0.
1=0.
∴![]() =
=![]() .
.
∴点B的坐标为(![]() ,0),OB=
,0),OB=![]() .
.
∵![]() =0,∴
=0,∴![]() =01=1.
=01=1.
∴![]() =1.∴OC=1.
=1.∴OC=1.
∵sin∠OCB=![]() ,
,
∴∠OCB=30°.
∴tan∠OCB=![]() .
.
∴OB=![]() OC.
OC.
∴![]() =
=![]() ×1.
×1.
∴k=![]() .
.
∴B点坐标为(![]() ,0),k的值为
,0),k的值为![]() .
.
(2)过点A作AH⊥x轴于H,如图.
则有AH=y=![]() x1.x>
x1.x>![]() .
.
∴S=![]() OBAH=
OBAH=![]() ×
×![]() ×(
×(![]() x1)=
x1)= ![]()
![]() ,(x>
,(x>![]() ).
).
(3)当S△AOB=![]() 时,
时, ![]()
![]() =
=![]() .
.
解得;x=![]() .
.
∴y=![]() x 1=
x 1=![]() ×
×![]() 1=
1=![]() .
.
∴点A的坐标为(![]() ,
,![]() ).
).
∴当点A运动到点(![]() ,
,![]() )的位置时,△AOB的面积是
)的位置时,△AOB的面积是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】仔细观察下面的正四面体、正六面体、正八面体,解决下列问题:
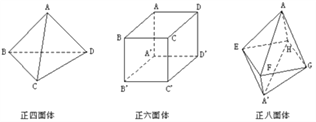
⑴填空:
①正四面体的顶点数V= ,面数F= ,棱数E= .
②正六面体的顶点数V= ,面数F= ,棱数E= .
③正八面体的顶点数V= ,面数F= ,棱数E= .
⑵若将多面体的顶点数用V表示,面数用F表示,棱数用E表示,则V、F、E之间的数量关系可用一个公式来表示,这就是著名的欧拉公式,请写出欧拉公式:
⑶如果一个多面体的棱数为30,顶点数为20,那么它有多少个面?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.
(1)试求抛物线的解析式;
(2)直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m=![]() ,试求m的最大值及此时点P的坐标;
,试求m的最大值及此时点P的坐标;
(3)在(2)的条件下,点Q是x轴上的一个动点,点N是坐标平面内的一点,是否存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形?如果存在,请求出点N的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣2,4),过点A作AB⊥y轴,垂足为B,连结OA.
(1)求△OAB的面积;
(2)若抛物线y=﹣x2﹣2x+c经过点A,求c的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四座城市A,B,C,D分别位于一个边长100km的大正方形的四个顶点,由于各城市之间的商业往来日益频繁,于是政府决定修建公路网连接它们,根据实际,公路总长设计得越短越好,公开招标的信息发布后,一个又一个方案被提交上来,经过初审后,拟从下面四个方案中选定一个再进一步认证,其中符合要求的方案是( )




A. B. C. D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个长为![]() ,宽为
,宽为![]() 的长方形内,该长方形内部未被卡片覆盖的部分用阴影表示.
的长方形内,该长方形内部未被卡片覆盖的部分用阴影表示.
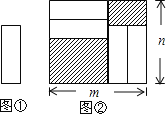
(1)能否用只含![]() 的式子表示出图②中两块阴影部分的周长和?_____(填“能”或“不能”);(2)若能,请你用只含
的式子表示出图②中两块阴影部分的周长和?_____(填“能”或“不能”);(2)若能,请你用只含![]() 的式子表示出中两块阴影部分的周长和;若不能,请说明理由_____.
的式子表示出中两块阴影部分的周长和;若不能,请说明理由_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
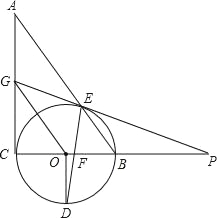
【题目】如图,Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于E,OD⊥BC交⊙O于D,DE交BC于F,点P为CB延长线上的一点,PE延长交AC于G,PE=PF,下列4个结论:①GE=GC;②AG=GE;③OG∥BE;④∠A=∠P.其中正确的结论是_____(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地台风带来严重灾害,该市组织20辆汽车装食品、药品、生活用品三种救灾物质共100吨到灾民安置点.按计划20辆汽车都要装运,每辆汽车只能装运同种物质且必须装满.根据表格提供的信息,解答下列问题:
物资种类 | 食品 | 药品 | 生活用品 |
每辆汽车运载量(吨) | 6 | 5 | 4 |
每吨所需运费(元/吨) | 120 | 160 | 100 |
(1)若装食品的车辆是5辆,装药品的车辆为__________辆;
(2)设装食品的车辆为x辆,装药品的车辆为y辆,求y与x的函数关系式;
(3)如果装食品的车辆不少于7辆,装药品的车辆不少于4辆,那么车辆的安排有几种方案?请写出每种方案并求出最少费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com