
【题目】某地台风带来严重灾害,该市组织20辆汽车装食品、药品、生活用品三种救灾物质共100吨到灾民安置点.按计划20辆汽车都要装运,每辆汽车只能装运同种物质且必须装满.根据表格提供的信息,解答下列问题:
物资种类 | 食品 | 药品 | 生活用品 |
每辆汽车运载量(吨) | 6 | 5 | 4 |
每吨所需运费(元/吨) | 120 | 160 | 100 |
(1)若装食品的车辆是5辆,装药品的车辆为__________辆;
(2)设装食品的车辆为x辆,装药品的车辆为y辆,求y与x的函数关系式;
(3)如果装食品的车辆不少于7辆,装药品的车辆不少于4辆,那么车辆的安排有几种方案?请写出每种方案并求出最少费用.
【答案】(1)10;(2)y= -2x+20;(3)安排方案有2种:方案一:装运食品7辆、药品6辆,生活用品7辆;方案二:装运食品8辆、药品4辆,生活用品8辆.最少费用为12160元.
【解析】
(1)设装药品的车辆数为x辆,则装运生活用品的车辆数为(20-5 -x),根据三种救灾物资共100吨列出方程即可求解;
(2)装运生活用品的车辆数为(20-x-y),根据三种救灾物资共100吨列出关系式;
(3)根据题意求出x的取值范围并取整数值从而确定方案;分别表示装运三种物质的费用,求出表示总运费的表达式,运用函数性质解答.
解:(1)设装药品的车辆数为x辆,则装运生活用品的车辆数为(20-5 -x),由题意,得
5×6+5x+4(20-5-x)=100
解得:x=10,
答:装药品的车辆为10辆;
(2)根据题意,装运食品的车辆数为x,装运药品的车辆数为y,
那么装运生活用品的车辆数为(20-x-y),
则有6x+5y+4(20-x-y)=100,
整理得,y= -2x+20;
(3)由(2)知,装运食品,药品,生活用品三种物资的车辆数分别为x,20-2x,x,
由题意,得![]() ,
,
解这个不等式组,得7≤x≤8,
因为x为整数,所以x的值为7,8.
所以安排方案有2种:
方案一:装运食品7辆、药品6辆,生活用品7辆;
方案二:装运食品8辆、药品4辆,生活用品8辆.
设总运费为W(元),
则W=6x×120+5(20-2x)×160+4x×100
=16000-480x,
因为k=-480<0,所以W的值随x的增大而减小.
要使总运费最少,需x最大,则x=8.
故选方案二.
W最小=16000-480×8=12160元.
最少总运费为12160元.
故答案为:(1)10;(2)y= -2x+20;(3)安排方案有2种:方案一:装运食品7辆、药品6辆,生活用品7辆;方案二:装运食品8辆、药品4辆,生活用品8辆.最少费用为12160元.


科目:初中数学 来源: 题型:
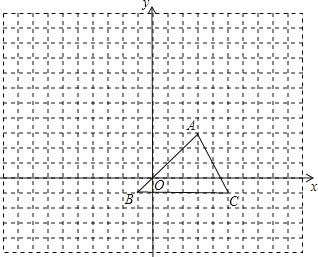
【题目】如图,直线y=kx-1与x轴、y轴分别交于B、C两点,OB:OC=![]() .
.
(1)求B点的坐标和k的值.
(2)若点A(x,y)是第一象限内的直线y=kx-1上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;
(3)在(2)的条件下,当点A运动到什么位置时,△AOB的面积是![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.

(1)求证:△ODE∽△ECF;
(2)在点O的运动过程中,设DE= ![]() :
:
①求![]() 的最大值,并求此时⊙O的半径长;
的最大值,并求此时⊙O的半径长;
②判断△CEF的周长是否为定值,若是,求出△CEF的周长;否则,请说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某一城市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天,乙队单独完成这项工程需要90天;若由甲队先做20天,剩下的工程由甲、乙两队合做完成.
(1)甲、乙两队合作多少天?
(2)甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△AOB是直角三角形,∠AOB=90°,边AB与y轴交于点C.

(1)若∠A=∠AOC,试说明:∠B=∠BOC;
(2)延长AB交x轴于点E,过O作OD⊥AB,若∠DOB=∠EOB,∠A=∠E,求∠A的度数;
(3)如图,OF平分∠AOM,∠BCO的平分线交FO的延长线于点P,∠A=40°,当△ABO绕O点旋转时(边AB与y轴正半轴始终相交于点C),问∠P的度数是否发生改变?若不变,求其度数;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格,△ABC的顶点在网格上,在建立平面直角坐标系后,点B的坐标是(-1,-1)
(1)把△ABC向左平移10格得到![]() ,画出
,画出![]() ;
;
(2)画出![]() 关于x轴对称的图形
关于x轴对称的图形![]() ;
;
(3)把△ABC绕点C顺时针旋转90°后得到![]() ,画出
,画出![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.

(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网上书城“五一·劳动节”期间在特定的书目中举办特价促销活动,有A、B、C、D四本书是小明比较中意的,但是他只打算选购两本,求下列事件的概率:
(1)小明购买A书,再从其余三本书中随机选一款,恰好选中C的概率是_________;
(2)小明随机选取两本书,请用树状图或列表法求出他恰好选中A、C两本的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是(一6,8).矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F.

(1)直接写出线段BO的长:
(2)求点D的坐标;
(3)若点N是平面内任一点,在x轴上是否存在点M,使咀M、N、E、O为顶点的四边形是菱形?若存在,请直接写出满足条件的点M的坐标:若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com