
【题目】在平面直角坐标系中,O是坐标原点,矩OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8),点P是y轴上的一个动点,将△OAP沿AP翻折得到:△O′AP,直线BC与直线O′P交于点E,与直线O′A交于点F.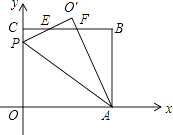
(1)当O′落在直线BC上时,求折痕AP的长.
(2)当点P在y轴正半轴上时,若△PCE与△POA相似,求直线AP的解析式;
(3)在点P的运动过程中,是否存在某一时刻,使得 ![]() ?若存在,求点P坐标;若不存在,请说明理由.
?若存在,求点P坐标;若不存在,请说明理由.
【答案】
(1)
解:图1,当O′落在直线BC上时,在RT△ABO′中,∵AO′=10,AB=8,
∴BO′= ![]() =
= ![]() =6,
=6,
∵△APO′是由△AOP翻折,
∴可以设PO=PO′=x,
在RT△PCO′中,∵PO′2=PC2+CO′2,
∴x2=(8﹣x)2+42,
∴x=5,
∴AP= ![]() =
= ![]() =5
=5 ![]()
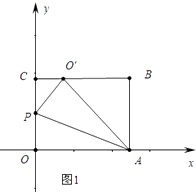
(2)
解:当∠CPE=∠APO时,
∵∠CPE=∠APO=∠APO′=60°,
∴OP= ![]() OA=
OA= ![]() ,
,
设直线AP为y=kx+b,由题意 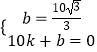 解得
解得 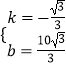 ,
,
∴直线AP为y=﹣ ![]() x+
x+ ![]() .
.
当∠CPE=∠OAP时,∠CEP=∠APO=∠APO′,此时AP∥EC,显然不可能
(3)
解:情形1如图2中,
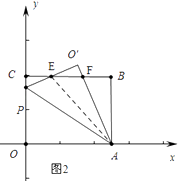
∵CE= ![]() BC=2,
BC=2,
∴BE=8,AE= ![]() =8
=8 ![]() ,EO′=
,EO′= ![]() =2
=2 ![]() ,
,
设OP=x,在RT△PCE中,∵PE2=PC2+CE2,
∴(x﹣2 ![]() )2=(8﹣x)2+22,
)2=(8﹣x)2+22,
∴x= ![]() ,此时P[0,
,此时P[0, ![]() ],
],
情形2如图3中,
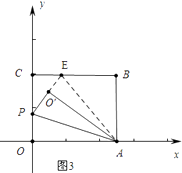
同理O′E=2 ![]() ,
,
设OP=x,在RT△PCE中,∵PE2=PC2+CE2,
∴(x+2 ![]() )2=(8﹣x)2+22,
)2=(8﹣x)2+22,
∴x= ![]() ,此时P[0,
,此时P[0, ![]() ],
],
情形3如图4中,
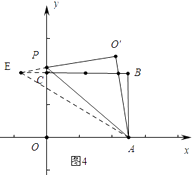
AE= ![]() =
= ![]() =4
=4 ![]() ,
,
EO′= ![]() =6
=6 ![]() ,
,
设OP=x,在RT△PCE中,∵PE2=PC2+CE2,
∴(6 ![]() ﹣x)2=(x﹣8)2+22,
﹣x)2=(x﹣8)2+22,
∴x= ![]() ,此时P[0,
,此时P[0, ![]() ],
],
情形4如图5中,
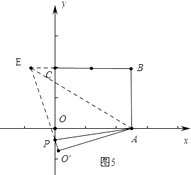
设OP=x,在RT△PCE中,∵PE2=PC2+CE2,
∴(6 ![]() ﹣x)2=(x+8)2+22,
﹣x)2=(x+8)2+22,
∴x= ![]() ,此时P[0,
,此时P[0, ![]() ].
].
【解析】(1)先在RT△ABO′求出BO′,设PO=PO′=x,在RT△PCO′中利用勾股定理解决即可.(2)当∠CPE=∠APO时得∠CPE=∠APO=∠APO′=60°求出OP= ![]() OA即可.当∠CPE=∠OAP时,∠CEP=∠APO=∠APO′,此时AP∥EC,显然不可能.(3)分四种情形讨论,在RT△PCE中利用E2=PC2+CE2列出方程求解 .
OA即可.当∠CPE=∠OAP时,∠CEP=∠APO=∠APO′,此时AP∥EC,显然不可能.(3)分四种情形讨论,在RT△PCE中利用E2=PC2+CE2列出方程求解 .
【考点精析】解答此题的关键在于理解相似三角形的性质的相关知识,掌握对应角相等,对应边成比例的两个三角形叫做相似三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知点A在数轴上对应的数为a,点B在数轴上对应的数为b,且|a+3|+|b-2|=0,A,B 之间的距离记为|AB|.请回答问题:
(1)直接写出a,b, |AB|的值. a= ,b = , |AB|= ;
(2)设点P在数轴上对应的数为x,当|PA|-|PB|=2时,求x的值;
(3)若点P在点A的左侧,M、N分别是PA、PB的中点.当点P在点A的左侧移动时,式子|PN|-|PM|的值是否发生改变?若不变,请求出其值;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是初中数学的一个重要工具.利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b.
如图:
已知数轴上有A、B两点,分别表示的数为﹣10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).
(综合运用).
(1)点A运动2秒后所在位置的点表示的数为 ;点B运动3秒后所在位置的点表示的数为 ;
(2)它们按上述方式运动,A、B两点经过多少秒会相遇,相遇点所表示的数是什么?
(3)它们按上述方式运动,A、B两点经过多少秒后相距2个单位长度?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了( )
A. 10场 B. 11场 C. 12场 D. 13场
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).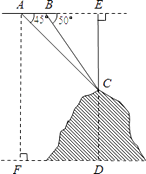
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P的坐标为(a,b),点P的“变换点”P`的坐标定义如下:当![]() 时,P`点坐标为(a,-b);当
时,P`点坐标为(a,-b);当![]() 时,P`点坐标为(b,-a)。线段l:
时,P`点坐标为(b,-a)。线段l:![]() 上所有点按上述“变换点”组成一个新的图形,若直线
上所有点按上述“变换点”组成一个新的图形,若直线![]() 与组成的新的图形有两个交点,则k的取值范围是( )
与组成的新的图形有两个交点,则k的取值范围是( )
A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.
(1)若AE=CF;
①求证:AF=BE,并求∠APB的度数;
②若AE=2,试求APAF的值;
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com